chemoleo - 8-10-2006 at 19:22
What is the number series of points on spheres that are equidistant to each other? I tried searching but to no avail.
For instance, the series is 2 (one point at the top, one at the bottom), then 4 (equidistant pyramid), 8 (cube), then ... what follows?
Lets say I want to have 40+ points on a sphere... what is the closest number where all are equidistant? No buckminster fullerenes, whatever, what I
desire here is that all points on the sphere have an equal distance to the next.
Any budding or real mathematicians who could help me?
If so, how can one draw this most efficiently on a physical sphere?
[Edited on 9-10-2006 by chemoleo]
12AX7 - 8-10-2006 at 20:01
Hmm, a regular polyhedron with surface composed of triangles would fit, no?
Tim
Elawr - 8-10-2006 at 20:16
It would be 1, 2, 4, 6, 8, 12, 20; these correspond to the number of vertices for the regular polyhedra. A cube for example can be enclosed by a
sphere with diameter equal to the distance between any 2 contralateral vertices. the cube's corners where they touch the inside of the sphere, make
8 equidistant points. same thing for the octahedron, icosahedron etc. Just so long as they be regular polyhedra.
[Edited on 9-10-2006 by Elawr]
chemoleo - 8-10-2006 at 20:44
Ok...so I specifically excluded '6' because it's essentially a double foursided pyramid right? A sqare, with one point above and one below. But the
distances of one of the corners of the square to the points above or below are not equal to the distances of the corner of the square to the next
corner of the square, right?
Looking at at the octahedron (6)

darn I am not so sure. It seems equal in length. What's the mathematical derivation for this?
You seem to be right for the icosahedron too (12)

How about the dodecahedron (20 by my count)
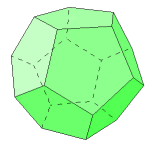
What follows after this?
Gahh.. they are called platonic solids...thanks for the clue
http://en.wikipedia.org/wiki/Platonic_solid
But now answer as to what follows...do I really have to get into the math?
Look at these animations...awesome!
http://ibiblio.org/e-notes/3Dapp/Convex.htm
Elawr - 8-10-2006 at 21:15
The icosahedron/dodecahedron duo are the highest regular polyhedra - that is, solids with identical faces and vertices, and all angles equal. You
don't really need heavy math - imagine a hollow sphere in zero G with 20 smaller spheres of equal negative (or positive charge) free to move inside.
They will tend to come to rest in a configuration corresponding to the vertices of the dodecahedron. What are you trying to do anyway, frame up a
geodesic dome in your backyard?
[Edited on 9-10-2006 by Elawr]
chemoleo - 9-10-2006 at 08:51
That's an interesting thought experiment, Elawr. I wonder what would happen if you chucked in 40+ of such repellent small spheres inside a big sphere?
What optimal positions would they take? How can I work this out?
No dome or anything. If it works, you'll be hearing about it 
YT2095 - 9-10-2006 at 08:58
YT2095 is a little worried by this whole line of questioning and wonders if Chemoleo plans his OWN N. Korea type experiment! 
chemoleo - 9-10-2006 at 09:04
Lol... I didn't mean the 'hearing' bit literally! 

12AX7 - 9-10-2006 at 09:11
Close packing gets you an hcp structure, for starters. Most of it is going to look hcp. If you don't need it centered on the origin, you can
probably fit slightly more spheres inside an arbitrary bounding sphere than a symmetrical hcp structure.
Tim
chemoleo - 9-10-2006 at 09:47
Hexagonal Close Packing (hcp).... I am not intending close packing. Imagine the sphere is 10 cm across, with the points being 5 mm in size each.
Plenty of space to arrange 40 of them in an unconstrained way.
indigofuzzy - 13-10-2006 at 08:41
wouldn't 3 points arranged in an equillateral triangle also be equidistant around a sphere? or not?
I'll give some thought to this, because I've been wondering about the same question - in relation to spherical ambisonic surround sound.
Elawr - 30-10-2006 at 09:29
I think if you had 40 unconstrained in a sphere they would come to rest in any of several possible metastable configurations. I don't think the
geometry would allow all 40 to be exactly equidistant but I can't prove this. Need a brain of considerably higher wattage than my own to figure that
one out. I think you'd get some kind of symmetrical pattern.
This is very interesting topic, and pertinant, since it describes behaviors of such things as shapes of atomic orbitals, coordination complexes, and
such.
JohnWW - 30-10-2006 at 10:15
The icosahedron is the finite regular solid with the greatest number of regular polygonal faces all of one type, due to the fact that it is the one
formed from the smallest and most angular polygons, triangles, with the greatest number of polygons sharing common vertices to subtend less than an
180º angle at each vertex and thereby enclose space. This was noted by the ancient Greek mathematicians.
Beyond this, there are only infinite tesselations all of one type of regular polygon, to form infinite planes, which are possible only with regular
triangles, squares, and hexagons. There are also "semi-regular" finite polyhedra and infinite tesselations, consisting of either two different regular
polygons as in the case of the soccer-ball or fullerene molecule (C60) which consist of hexagons and pentagons, or also truncated (at vertices)
regular polyhedra, or having more than one dihedral angle as in the case of stellated regular polyhedra (e.g. the stellated dodecahedron which has 60
regular triangles), or infinite tesselations consisting of two types of regular polygons e.g. octagons plus triangles and hexagons plus triangles.
solo - 30-10-2006 at 11:14
Reference Information Interesting Reading
The Fitting Polynomial to Equidistant Data with Missing Values
H.O. Hartley
Biometika vol.38,no. 3/4, pp. 410-413, 1951
---------------------------------------------------------------------------------------
The distribution of points on the sphere and corresponding cubature formulae
Jorg Fliege and Ulrike Maier
IMA Journal of Numerical Analysis nu.19, pp.317-334, 1999
Attachment: point distribution formulas.zip (1.1MB)
This file has been downloaded 380 times