| Pages:
1
..
11
12
13
14
15
..
19 |
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Oh bugger.
I remember that formula (vaguely) from school, but did not recognise the derivative as a Quadratic equation.
Heigh-ho.
Got it half right, which is pretty good for a Saturday !
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
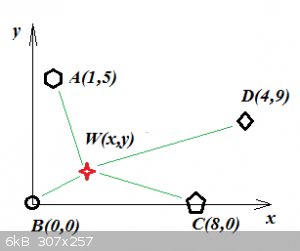
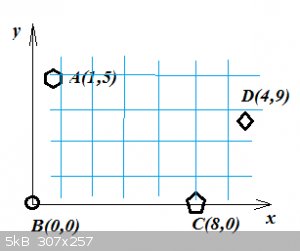
Minimum distance problem:
A planner for Vulture Chemicals plots a grid on a map and determines that VC’s four most important customers are located at A(1, 5), B(0, 0), C(8,
0) and D(4,9) where units are in 100 miles. At what point W(x, y) should a warehouse be located in order to minimize the sum of the distances from W
to A, B, C, and D?
Preamble:
In a Cartesian coordinate system the distance between two points:
$$(x_1,y_1),(x_2,y_2)$$
... can be calculated as follows:
$$d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$$
For this problem it's easier to use the squares of the distances:
$$d^2=(x_1-x_2)^2+(y_1-y_2)^2$$
If S is the sum of the squares of the distances for all four customers to the planned warehouse:
$$S=\Sigma d^2$$
Then:
$$S(x,y)=[(x-1)^2+(y-5)^2]+(x^2+y^2)+[(x-8)^2+y^2]+[(x-4)^2+(y-9)^2]$$
By means of the partial derivatives fx and fy, find the minimum for S.
(This is the last optimisation problem. Next: famous second order DVs)
[Edited on 3-5-2016 by blogfast25]
|
|
|
woelen
Super Administrator
        
Posts: 7977
Registered: 20-8-2005
Location: Netherlands
Member Is Offline
Mood: interested
|
|
What you do is not equivalent. Minimizing the sum of distances in general need not give the same result as minimizing the sum of the squares of
distances. It may be that in this particular case the answer is the same (I did not do any math on this), but in general this certainly is not the
case.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Is this the S(x,y) = 0 thing ?
If so,
$$S(x,y)=[(x-1)^2+(y-5)^2]+(x^2+y^2)+[(x-8)^2+y^2]+[(x-4)^2+(y-9)^2]$$
$$=x^2-2x+1+y^2-10y+25+x^2+y^2+x^2-16x+64+y^2+x^2-8x+16+y^2-18y+81$$
$$=4x^2+4y^2-26x-28y+187$$
$$f_x = 8x-26, f_y = 8y-28$$
$$f_x = 0, x=\frac {26}{8} = 3.25$$
$$f_y = 0, y=\frac {28}{8} = 3.5$$
$$\therefore S(x,y) = 0 = S(3.25, 3.5)$$
It looks like point D should be (9, 4) where it is shown on the plot, rather than (4, 9).
@woelen: i think the excercise was made more interesting by having an actual application.
Whether it works or not is a moot point, especially if it's me doing the calculations !
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
@woelen; I'll address your point a little later on. Thanks!
@aga:
Correct!
But your final statement is not:
$$S(x,y) = 0 = S(3.25, 3.5)$$
The sum of the distances is far from zero. But fx=fy=0, for (3.25,3.5).
The D point was badly drawn, but the (4,9) coordinates were correct and as intended.
It's also a little quicker if you use the chain rule on terms like:
$$(x-4)^2$$
$$f_x=2(x-4) \times f_x(x-4)=2(x-4) \times 1=2(x-4)$$
Still, as they say: 'whatever works for you'.
[Edited on 3-5-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by woelen  | | What you do is not equivalent. Minimizing the sum of distances in general need not give the same result as minimizing the sum of the squares of
distances. It may be that in this particular case the answer is the same (I did not do any math on this), but in general this certainly is not the
case. |
You're correct.
If:
$$d_i=\sqrt{(x-x_i)^2+(y-y_1)^2}$$
Then:
$$S=\Sigma d_i=\Sigma_i \sqrt{(x-x_i)^2+(y-y_1)^2}$$
And:
$$f_x=\Sigma_i \frac{(x-x_i)}{\sqrt{(x-x_i)^2+(y-y_1)^2}}$$
$$f_y=\Sigma_i \frac{(y-y_i)}{\sqrt{(x-x_i)^2+(y-y_1)^2}}$$
Then that would not give the same results as we computed.
I found the exercise somewhere, made it a little harder but didn't stop to think. Grrr.  
[Edited on 3-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Teaching is a 2 way thing.
Maybe a little has rubbed off 
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Don't get me worried... 
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Famous second order DEs:
Newtonian equations of motion:
Consider an object of mass m on which a number of forces act, shown below are 3 forces:
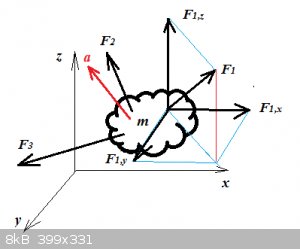
Then Newton’s Second Law tells us:
$$\Sigma_i \vec{F_i}=m\vec{a}$$
Worded: 'the vector sum of the acting forces equals the mass times the acceleration vector'
Analytically, this is usually solved by using the property that motions in the x, y and z directions are completely independent of each other. This
allows to break down the vector problem into three independent non-vector equations:
$$\Sigma_i F_{x,i}=ma_x$$
$$\Sigma_i F_{y,i}=ma_y$$
$$\Sigma_i F_{z,i}=ma_z$$
From now on we’ll drop the indices x, y and z because it is usually very clear from the context of the problem which axis is meant. Also we’ll
call:
$$\Sigma_i F_i=F$$
Where F is the sum of the force components along the intended axis, often also called the net force (along that axis).
So for a given axis we can now simply write:
$$ma=F$$
Also:
$$m\frac{dv}{dt}=F$$
And (for an x-axis):
$$m\frac{d^2x}{dt^2}=F$$
Specific examples:
1. F is constant:
Real world example: a free falling body (without drag).
$$m\frac{dv}{dt}=F$$
Integrate with boundary conditions t=0, v=v<sub>0</sub>, x=x<sub>0</sub>:
$$\int_{v_0}^v dv=\int_0^t \frac{F}{m}dt$$
$$\implies v(t)=v_0+\frac{F}{m}t$$
$$v(t)=\frac{dx(t)}{dt}=v_0+\frac{F}{m}t$$
Integrate again:
$$\int_{x_0}^xdx=\int_0^t(v_0+\frac{F}{m}t)dt$$
$$\implies x(t)=x_0+v_0t+\frac{F}{2m}t^2$$
2. F is a function of v:
$$ma=f(v)$$
$$m\frac{dv}{dt}=f(v)$$
Integrate:
$$m\int \frac {dv}{f(v)}=\int dt$$
Alternatively:
$$mx''(t)=f[x'(t)]$$
Real world example: projectile with drag. We derived such a problem higher up:
$$ma=mg-F_{drag}$$
Specifically:
$$v’=9.8-\frac{5v}{50}=9.8-\frac{v}{10}$$
We solved this by twice integrating, to obtain x(t).
But it can also be solved by writing it as:
$$\frac{d^2x}{dt^2}=9.8-\frac{1}{10}\frac{dx}{dt}$$
Or:
$$x''+0.1x'-9.8=0$$
The boundary conditions were:
$$t=0, x(0)=0, x'(0)=-10$$
I used Wolfram Alpha's DSolve function for this and obtained:
$$x(t)=98t+1080e^{-0.1t}-1080$$
Which is also what we found before.
[Edited on 3-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
In
$$\Sigma_i \vec{F_i}=m\vec{a}$$
what does the i signify ?
The arrows mean Vectors, although quite how they work is a mystery.
A bit of utoob showed a tail-to-tip example which made sense in isolation (vector addition).
Putting them into an equation, Fwooosh ! Straight over head.
Edit:
It is nice to see that Wolfram got it right as well 
Another thing: why is an accurate depiction of my brain being used in the example image ?
[Edited on 3-5-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | In
$$\Sigma_i \vec{F_i}=m\vec{a}$$
what does the i signify ?
The arrows mean Vectors, although quite how they work is a mystery.
A bit of utoob showed a tail-to-tip example which made sense in isolation (vector addition).
Putting them into an equation, Fwooosh ! Straight over head.
Edit:
It is nice to see that Wolfram got it right as well 
Another thing: why is an accurate depiction of my brain being used in the example image ?
|
i is the index (number) of a force, as in:
$$F_1,F_2,...,F_i,...,F_n$$
Vector calculation:
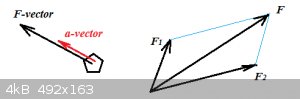
Right: an example of two vectors being added up.
Left: F would be the resultant vector from adding up all vectors on the brain:
$$\Sigma_i \vec{F_i}=\vec{F}$$
The acceleration vector
$$\vec{a}$$
... is obtained by:
$$\vec{a}=\frac{\vec{F}}{m}$$
Both F and a vectors thus are parallel and point in the same direction, they're simply different in size.
But as explained, usually we kind of avoid all that vectoring by looking at the x,y,z force components.
I'll post a simple example.
[Edited on 3-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
So in
$$\Sigma_i \vec{F_i}=\vec{F}$$
the meaning of
$$\vec{F}$$
is : "The sum of all i nvolved vectors"
Figuring out the Words is almost as hard as the maths.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | So in
$$\Sigma_i \vec{F_i}=\vec{F}$$
the meaning of
$$\vec{F}$$
is : "The sum of all i involved vectors"
Figuring out the Words is almost as hard as the maths. |
Yes!
Now hold your fire for 5 mins.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Object sliding down an incline:
Consider an object of mass m sliding down a smooth incline (angle theta), without friction or drag:
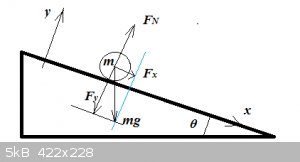
Carefully note the choice of x and y-axis, please.
What are the forces and accelerations in play?
The weight mg is decomposed into an x and a y-component.
y-axis:
$$F_y=-mg\cos \theta$$
This force is countered by a reaction force FN provided by the incline, so that:
$$F_N-mg\cos\theta=0$$
There's no NET force acting on the object in the y-direction.
$$\implies a_y=0$$
No acceleration in the y-direction.
x-axis:
$$F_x=mg\sin \theta$$
In the absence of friction or drag, Fx is also the ONLY force acting on the object along the x-axis, so:
$$ma_x=mg\sin\theta$$
$$\implies a_x=g\sin \theta$$
The object will accelerate along the x-axis with constant acceleration:
$$a_x=g\sin \theta$$
<hr>
Fun with a shopping trolley and two toddlers!
You're pushing a shopping trolley with force F1. Toddler 1 want to pull the trolley towards the chocolates with force F3, while
toddler 2 want to pull it to the toys, with force F2:
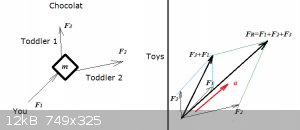
On the right we add up the force vectors, first F3 + F1, then add to that F2, to get the resultant ('net') force
FR.
The trolley will experience an acceleration vector a:
$$\vec{a}=\frac{\vec{F_R}}{m}$$
[Edited on 4-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Could the Distribution centre problem not be solved with vector maths ?
I.e. the distance being the Force, and the angle being the other bit of the vector.
I guess it'd get complicated finding a common solution, unless that's what vector derviatives are all about.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Let think about that.
Coming up, another example of a Newtonian equation of motion.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
I started thinking about working from the Centre and solving for each of the vector forces, then realised that the Centre is the actual answer.
Amazingly, over 10 years ago i posed this exact question on a freelance programmer's website to get a way to calculate the position of a mobile phone
tower based on GPS co-ordinates with TA values in order to map where all the mobile towers are.
TA=Timing Advance = 1 for every 550m your phone is away from the tower.
It's used for keeping phones at differing distances away from the tower in synch with the tower's timing chain.
The idea was to implement a non-GPS based positioning system based on Known tower sites.
Cheap too, as the GSM units do not even need a SIM card (=no contract) to get the TA information (phones MUST connect with no SIM to do 999/112
calls).
Never did get any useful solution, then they went and released the tower locations on a public website.
Contemporaneously Google released Google Maps which blew away all the vector mapping companies.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
3. F is a function of x:
Real world example: Simple Harmonic Oscillator.
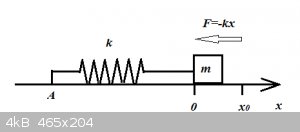
A massless Hookean spring with spring constant k is anchored at A and attached to an object of mass m. Ignore all friction or drag.
Initially the spring is neither extended nor compressed but at t=0 we move the object to x=x0, then release it. The restoring force exerted
by the spring is kx and the Newtonian equation is:
$$ma_x=-kx(t)$$
$$a_x=\frac{d^2x(t)}{dt^2}=x''(x)$$
$$mx''(t)+kx(t)=0$$
Or in 'shorthand':
$$mx''+kx=0$$
We assume the solution to be of the general form:
$$x=C_2\cos C_1 x$$
So:
$$x'=-C_2C_1 \sin C_1 x$$
$$x''=-C_2C_1^2\cos C_1 x$$
Plug it all into the DV:
$$-mC_2C_1^2\cos C_1 x+kC_2\cos C_1 x=0$$
C2cosC1x drops out and we get:
$$mC_1^2=k$$
$$C_1=\sqrt{\frac{k}{m}}$$
Now with the boundary condition:
$$t=0, x=x_0$$
$$\implies C_2=x_0\cos 0=x_0$$
So:
$$x(t)=x_0\cos \Big(\sqrt{\frac{k}{m}}t\Big)$$
C1 is often called the angular velocity, omega:
$$\omega=\sqrt{\frac{k}{m}}$$
The frequency of oscillation is:
$$f=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$$
The period of oscillation is:
$$T=\frac1f$$
<hr>
Would it matter if we rotate the whole set up, axis included, clockwise by 90 degrees? The object would then be hanging off the spring.
Let's see. The Newtonian equation now is:
$$ma=mg-kx(t)$$
$$mx''(t)+kx(t)-mg=0$$
$$mx''(t)+k[x(t)-\frac{mg}{k}]=0$$
Substitute:
$$u=x(t)-\frac{mg}{k}$$
$$u'=x'(t)$$
$$u''=x''(t)$$
$$mu''+ku=0$$
The derivation is the same as above and yields:
$$x(t)=\Big(x_0-\frac{mg}{k}\Big)\cos \Big(\sqrt{\frac{k}{m}}t\Big)$$
So gravity doesn't affect angular velocity, frequency or period of oscillation. Only amplitude is affected.
[Edited on 4-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Wow !
I assumed Gravity would have an effect on the frequency, although that may be due to naturally shoving friction in there.
[Edited on 4-5-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
Amazingly, over 10 years ago i posed this exact question on a freelance programmer's website to get a way to calculate the position of a mobile phone
tower based on GPS co-ordinates with TA values in order to map where all the mobile towers are.
|
There's a numerical solution to the minimum distance problem.
Create a Cartesian x,y grid (shown in blue) and calculate the sum of distances for each x,y point. A visual inspection (or Excel triage) will show you
where you are near to the optimum (x,y) point. Repeat with a finer mesh x,y grid in that area, for greater precision.
Quote: Originally posted by aga  | Wow !
I assumed Gravity would have an effect on the frequency, although that may be due to naturally shoving friction in there.
[Edited on 4-5-2016 by aga] |
There are numerous applications of SHOs (see e.g. pendulum clocks) and some with engineered friction, like a car's shock absorbers which provides a
critically damped SHO:
http://hyperphysics.phy-astr.gsu.edu/hbase/oscda2.html
In such a device the initial perturbation x0 is absorbed and then the system returns to x=0 as soon as possible.
The idealised DV is:
$$mx''+kx-g=\epsilon x'$$
... because the friction force is:
$$F_F=\epsilon v=\epsilon x'$$
[Edited on 5-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
I imagined the solution would be simpler in polar co-ordinates, seeing as the Location and Distance are the 'known' elements.
Perhaps that's why it never got figured out properly.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | I imagined the solution would be simpler in polar co-ordinates, seeing as the Location and Distance are the 'known' elements.
Perhaps that's why it never got figured out properly. |
Polar coordinates wouldn't help at all here. And distance is definitely an unknown element here...
More about the facility location problem, here: it's hard and has been from about 1860! 
[Edited on 5-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Sorry, i was thinking about the mobile phone towers problem there.
The TA value is basically a discrete integer representing a 550m increment per step : basically the distance to the the tower with crappy granularity.
So the two known values would be GPS co-odinates of the A,B,C,D locations, each with a known TA (=crappy granuarity distance) from the central point
= (The tower).
Problem was to calculate the GPS co-ordinates of that central point from a set of n GPS readings and measured TA values.
The geometry kind of suggested that at least 3 readings from varied positions would be needed to get an actual 'fix'.
Edit: these were the considered cases :
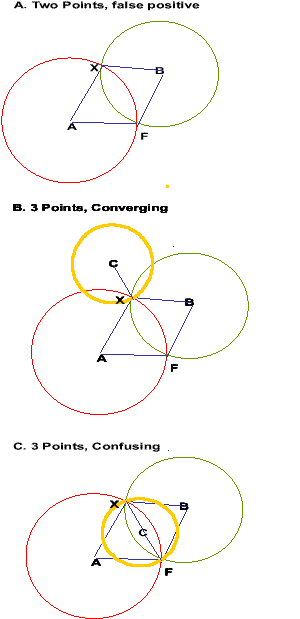
'X' marks the tower spot.
A,B, C are the known positions, the radius from each being the known distance to X.
F is the false positive, it being the same distance from A and B.
[Edited on 5-5-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
The Schrödinger equation (SE):
No mini-Pantheon of famous second order DEs can be complete without one of the most successful physics equations ever. Here it is again,
time-independent and for one dimension only:
$$-\frac{\hbar^2}{2m}.\frac{d^2\psi(x)}{dx^2}+V(x)\psi(x)=E\psi(x)$$
Now let’s see if with our new-found calculus ability we can analytically solve the simplest of all quantum problems: a particle in a one dimensional
box (Pi1DB, see also the QP thread):
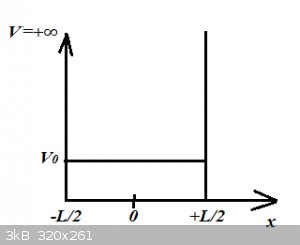
Mathematically:
$$-\frac{L}{2} \leq x\leq +\frac{L}{2}\:\text{then}\: V=V_0$$
$$|x| > \frac{L}{2} \:\text{then}\: V=+\infty$$
So the SE becomes:
$$-\frac{\hbar^2}{2m}.\frac{d^2\psi(x)}{dx^2}+V_0\psi(x)=E\psi(x)$$
Or:
$$-\frac{\hbar^2}{2m}.\frac{d^2\psi(x)}{dx^2}=(E-V_0)\psi(x)$$
So we’re looking for a function that twice derived kind of, sort of looks like the negative of itself. That’s quite reminiscent of:
$$(\sin x)'=\cos x$$
$$(\cos x)'=-\sin x$$
Or:
$$-(\sin x)''=\sin x$$
So we tentatively propose a solution of the form:
$$\psi=A\sin kx$$
$$\psi'=Ak\cos kx$$
$$\psi''=-Ak^2\sin kx$$
Plug it all into the SE:
$$-\frac{\hbar^2}{2m}(-Ak^2\sin kx)=(E-V_0)A\sin kx$$
$$\frac{\hbar^2}{2m}k^2=(E-V_0)$$
So it seems to be a fit but what are k and A?
We know that:
$$x=+\frac{L}{2}\implies \psi=0$$
$$\implies A\sin \Big(k\frac{L}{2}\Big)=0$$
And because:
$$A \neq 0$$
$$\implies \frac{kL}{2}=2\pi n$$
$$n=1,2,3,...$$
So:
$$k=\frac{4\pi n}{L}$$
$$\psi=A\sin \Big(\frac{4\pi n}{L}x\Big)$$
Also:
$$E_n=V_0+\frac{8\pi^2\hbar^2n^2}{mL^2}$$
To find A we need to apply the Normalisation condition:
$$\int_{-L/2}^{+L/2}\psi^2dx=1$$
$$\int_{-L/2}^{+L/2}\big[A\sin \Big(\frac{4\pi n}{L}x\Big)\Big]^2dx=1$$
It’s a banal integral which I’ll leave for readers to check, which yields:
$$A=\sqrt{\frac{2}{L}}$$
$$\psi_n(x)=\sqrt{\frac{2}{L}}\sin \Big(\frac{4\pi n}{L}x\Big)$$
First 8 wave functions (not to scale):
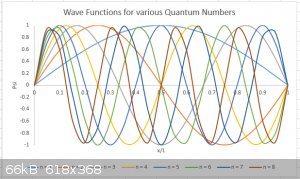
[Edited on 6-5-2016 by blogfast25]
[Edited on 6-5-2016 by blogfast25]
|
|
|
The Volatile Chemist
International Hazard
    
Posts: 1981
Registered: 22-3-2014
Location: 'Stil' in the lab...
Member Is Offline
Mood: Copious
|
|
This thread suddenly passed my level of knowledge, haha. I just took my AP Calculus AB test for university credit yesterday. Good stuff.
|
|
|
| Pages:
1
..
11
12
13
14
15
..
19 |