| Pages:
1
..
15
16
17
18
19 |
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
3.
$$f=[\cos (2x)+3]^4$$
$$g=\cos (2x)+3, f=g^4$$
$$(\cos (2x)+3)'.\Big((\cos (2x)+3)^4\Big)'$$
$$-\sin (2x).4(\cos (2x)+3)^3 = -4\sin (2x)(\cos (2x)+3)^3$$
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
4.
$$f=\sqrt [5]{1-2x}$$
$$g=1-2x, f=\sqrt [5] g, f=g^{\frac15}$$
$$(1-2x)'.\Big((1-2x)^{\frac15}\Big)'$$
$$=-2. \frac 15 (1-2x) ^{-\frac 45}$$
$$=\frac {-2}{5} \Big( \frac {1}{\sqrt [5]{1-2x}}\Big)^4 $$
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
5.
$$f=\sin\Big(\ln x+\frac{1}{x^2}\Big)$$
$$g=\ln x+\frac{1}{x^2} = \ln x +x^{-2}$$
$$\sin\Big(\ln x+\frac{1}{x^2}\Big)'.(\ln x +x^{-2})'$$
$$=\cos\Big(\ln x+\frac{1}{x^2}\Big). (\frac 1x -2x^{-3})$$
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
6.
$$f=\sqrt [3] {2x^4-x^2-3}$$
$$g=2x^4-x^2-3$$
$$(\sqrt [3] {2x^4-x^2-3})'.(2x^4-x^2-3)'$$
$$= (({2x^4-x^2-3})^\frac 13)'.(8x^3-2x)$$
$$= \frac 13 (2x^4-x^2-3)^{-\frac 23}.(8x^3-2x)$$
$$= \frac {8x^3-2x}{3} \Big( \frac {1}{\sqrt [3] {(2x^4-x^2-3)}} \Big)^2 $$
$$= \frac {8x^3-2x}{3} \frac {1}{(2x^4-x^2-3)^{\frac 23}} $$
$$= \frac {8x^3-2x}{3(2x^4-x^2-3)^{\frac 23}} $$
[Edited on 24-5-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
2.
$$\Big(\frac{1}{1+x}\Big)' = \Big((1+x)^{-1}\Big)' = -1(x+1)^{-2} = \frac {2}{-1(x+1)} = -\frac{2}{x+1}$$
... is correct up to and including the second identity. Then, for unknown reasons you turn the - 2 exponent into a coefficient!
Correct answer:
$$(x+1).-1(x+1)^{-2}=-(x+1)^{-1}=\frac{1}{1-x}$$
3.
$$-\sin (2x).4(\cos (2x)+3)^3 = -4\sin (2x)(\cos (2x)+3)^3$$
Correct apart from one minor mistake:
$$(\cos (2x)+3)'=(\cos(2x))'+0=-2\sin(2x)$$
The cos(2x) also needed chain ruling!
4. is correct.
5. is also correct.
6. is also correct and nicely reworked.
<hr>
Seems to me the chain gremlins have been dealt a lethal blow and apart from one or two still bleeding out, we won't hear from them again! 
Remember also that for simple functions:
$$f(g)=\cos g, \sin g, e^g, \ln g, g^n$$
If (with a and b constants):
$$g(x)=ax\:\text{...OR...}\:g(x)=ax+b$$
Then:
$$\frac{dg}{dx}=a$$
So:
$$f'(x)=a\frac{df(g)}{dg}$$
e.g.:
$$f(x)=\sin(ax+b)$$
$$f'(x)=a\cos(ax+b)$$
These are the simplest but also most frequently encountered cases of Chain Rule application!
[Edited on 24-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
(blush)
Yes, it does seem a lot clearer now.
Basically, if something happens to x (e.g. x+1, x^2, 3x+5 etc) then something happens to the result of that, then you need to use the chain
rule.
Still not comfortable with dg/dx etc but it feels like it's coming together.
Thanks again for taking the time to check these answers !
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Not entirely sure what you mean there. The whole Chain Rule business can be proved from the limit theorem.
For a function:
$$f\big(g(x)\big)$$
Then:
$$[f\big(g(x)\big)]'=\lim_{\Delta x \to 0}\frac{f\big(g(x+\Delta x)\big)-f\big(g(x)\big)}{\Delta x}$$
How this leads to:
$$[f\big(g(x)\big)]'=\frac{df(g)}{dg(x)}\times \frac{dg(x)}{dx}$$
... can be found in this formal proof:
http://kruel.co/math/chainrule.pdf
Enjoy! 
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
if the same brain can 'hear' the sound of that brain imploding, i just heard it.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
OK. You've cited Limit Theorem about 3 times now.
Best come clean and unload.
What's Limit Theorem all about ?
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | OK. You've cited Limit Theorem about 3 times now.
Best come clean and unload.
What's Limit Theorem all about ? |
It would have been more correct for me to refer to the 'limit definition of derivatives' (it's not really a theorem  ): ):
$$f'(x)=\frac{df}{dx}=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$$
All the rules of derivation (sum/difference, product, quotient, chain,...) can be derived from that simple principle.
Here are the actual computations of these limits (i.e. first derivatives) of a few simple functions:
https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/defderd...
(most of them require rather boring and lengthy algebra but aren't really that hard)
But in real life we simply use tabled derivatives of simple functions and the derivation rules for more complicated ones, instead of using the harder
limit taking route.
[Edited on 25-5-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Ooopsie. Double post deleted.
[Edited on 30-5-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Second order DEs (continued) (II):
In the previous post we saw that for a second order DE of the type:
$$ay''+by'+cy=0\:\text{, where: }y=f(x)$$
... a Chracteristic Equation (CE) can be defined as:
$$a\lambda^2+b\lambda +cy=0$$
The roots of this quadratic equation will be used to determine a full solution of the DE.
The two roots of the CE are determined from:
$$\lambda_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
We can now distinguish several cases:
1. Two Real and distinct roots:
If:
$$b^2-4ac>0$$
Then both roots are Real and distinct and the general solution of the DE is given by:
$$y=c_1e^{\lambda_1 x}+c_2e^{\lambda_2 x}$$
Where c1 and c2 are two integration constants, to be determined from boundary conditions.
An example was shown in the previous post.
2. Two Complex and distinct roots:
If:
$$b^2-4ac<0$$
Then note that the square root of that expression becomes Complex (imaginary):
$$\sqrt{b^2-4ac}=\sqrt{(4ac-b^2) \times -1}=\sqrt{4ac-b^2}\sqrt{-1}$$
Traditionally we call:
$$i=\sqrt{-1}$$
If in addition we set:
$$\beta =\frac{-b}{2a},\gamma = \frac{\sqrt{4ac-b^2}}{2a}$$
Then the Complex and distinct roots can be written as:
$$\lambda_{1,2} = \beta \pm \gamma i$$
We can then insert these roots into the general solution as above but that yields a complex function.
But using Euler's Formula and with some reworking (not shown here) we then obtain a Real solution:
$$y=c_1e^{\beta x}\cos \gamma x+c_2e^{\beta x}\sin \gamma x$$
Where c1 and c2 are two integration constants, to be determined from boundary conditions.
<hr>
Two more cases to follow:
$$b^2-4ac=0\:\text{and }b=0$$
[Edited on 30-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Gulp !
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Just try it for:
$$y''-4y'+5y=0\:\text{where: }y=f(x)$$
The CE has two complex roots. No boundary conditions have been given with the DE, so you don't need to determine values for the integration constants.
[Edited on 30-5-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Ct'ued from above:
For:
$$ay''+by'+cy=0$$
3. Repeat Real roots if:
$$b^2-4ac=0$$
$$\lambda_{1,2}=\frac{-b}{2a}=\lambda$$
$$\implies y=c_1e^{\lambda x}+c_2xe^{\lambda x}$$
Example/exercise:
$$y''+2y'+y=0$$
$$b^2-4ac=2^2-4.1.1=0$$
$$\implies \lambda=-\frac{b}{2a}=-\frac22=-1$$
Solution:
$$y=c_1e^{-x}+c_2xe^{-x}$$
Special case: b = 0
$$b=0 \implies \beta =0, \gamma = \sqrt{\frac{c}{a}}$$
a. Real roots:
$$\implies y=c_1e^{\lambda x}+c_2xe^{\lambda x}$$
b. Complex roots:
$$\implies y=c_1\cos \gamma x+c_2\sin \gamma x$$
<hr>
Coming up: a partial differential equation that makes music!
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Music notes!

Ever wondered why a plucked guitar string sounds the way it does? How precisely it vibrates? It’s a surprisingly cool calculus problem. It’s also
a big derivation, so we’ll do it in bite-size chunks.
Imagine a flexible string with linear density ρ (kg/m) clamped between x=0 and x=L, with a tension T:
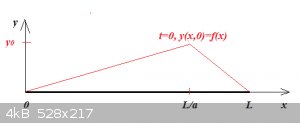
The string is deformed at time t=0 as shown by the red line, then released.
Mathematically the motion the string will assume is governed by the wave equation, partial differential equation (PDE):
$$\frac{\partial^2y}{\partial t^2}=\frac{T}{\rho}\frac{\partial^2y}{\partial x^2}$$
Where y is the displacement of a mass element of the string, as a function of x and t:
$$y(x,t)$$
Also we call:
$$\frac{T}{\rho}=c^2$$
(A full derivation of the PDE can be found here. It’s quite simple)
So:
$$\frac{\partial^2y}{\partial t^2}=c^2\frac{\partial^2y}{\partial x^2}$$
We also need some initial conditions:
$$y(x,0)=f(x)\:\text{and }\frac{\partial y(x,0)}{\partial t}=0$$
The left one describes the string’s position at t=0 (don’t worry about f(x) just yet) and the right one the string’s initial velocity (in the
y-direction), that is zero.
And some boundary conditions:
$$y(0,t)=0\:\text{and }y(L,t)=0$$
These represent the fact that the string is clamped at 0 and L and thus y=0 at all times in these points.
Ok, so far so good (and so little!) For solving this type of equations, as for DEs in general, no exact recipe exists. Instead a mixture of known
techniques, useful theorems and a good dollop of guesswork are used. Here we’ll try separation of variables for a starter: that means separating all
the xs from all the ts.
To do so, we make an important assumption:
$$y(x,t)=\phi(x)h(t)$$
Where φ(x) and h(t) are separate functions, resp. in x and t. Our sought after function y(x,t) is then presumed to be the product of the two,
φ(x)h(t).
Firstly, we insert the original boundary conditions into the proposed solution, so we get:
$$y(0,t)=\phi(0)h(t)=0\:\text{and }y(L,t)=\phi(L)h(t)=0$$
And assuming:
$$h(t) \neq 0$$
We get the boundary conditions for φ(x):
$$\phi(0)=0\:\text{and }\phi(L)=0$$
Next we plug the proposed solution y=(x,t)= φ(x)h(t) into the original PDE.
$$\frac{\partial^2}{\partial t^2}\big(\phi(x)h(t)\big)=c^2\frac{\partial^2}{\partial x^2}\big(\phi(x)h(t)\big)$$
This look a lot scarier than it is because of course φ(x) is independent of t and h(t) is independent of x, so both can be multiplied out of the
resp. derivatives. That also means we can dispense with the partial derivatives and we obtain:
$$\phi(x)\frac{d^2h}{dt^2}=c^2h(t)\frac{d^2\phi}{dx^2}$$
Minimal reworking yields separation of variables:
$$\frac{1}{c^2h}\frac{d^2h}{dt^2}=\frac{1}{\phi}\frac{d^2\phi}{dx^2}$$
Nice, huh? Hmmm... more like a ‘nice mess’, right now. And still no idea if this is even going to lead to a comprehensive solution of the PDE.
Stay tuned!
[Edited on 9-6-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
I'm starting to understand what they mean when they say a formula has a certain 'beauty'.
These hieroglyphs are incredible !
They look more like Art than Maths.
[Edited on 9-6-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | I'm starting to understand what they mean when they say a formula has a certain 'beauty'.
These hieroglyphs are incredible !
They look more like Art than Maths.
|
Yes. Trust me, it gets more beautiful as we get on with this problem.
The 'hieroglyphs' could be avoided by a notation we used above, for example:
$$\frac{\partial^2u}{\partial x^2}=u_{xx}$$
The wave equation then becomes:
$$y_{tt}=c^2y_{xx}$$
But that doesn't have the same allure. It is much more practical though...
[Edited on 9-6-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Aspersions cast i not, young 25 of blogfastingness.
The drawn glyphs admire i, and that muchly.
Of great beauty they are.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Music notes! (Ct'nued)
So far we obtained:
$$\frac{1}{c^2h}\frac{d^2h}{dt^2}=\frac{1}{\phi}\frac{d^2\phi}{dx^2}$$
This is really a bit of a strange animal. h(t) and φ(x) are obviously not the same (they’re not even dependent on the same variable!). This can
only make sense mathematically if both derivative equations (each side of the equation) equals the same number:
$$\frac{1}{c^2h}\frac{d^2h}{dt^2}=\frac{1}{\phi}\frac{d^2\phi}{dx^2}=-\lambda$$
Here λ is called the separation constant. The negative sign is for convenience (in some other PDEs a positive sign is needed, it’s case dependent)
Note that we don’t know its value yet though.
<hr>
We can now split the PDE into two parts (two DEs). First part:
$$\frac{1}{c^2h}\frac{d^2h}{dt^2}=-\lambda$$
Which reworks to:
$$\frac{d^2h}{dt^2}+c^2\lambda h=0$$
Second part:
$$\frac{1}{\phi}\frac{d^2\phi}{dx^2}=-\lambda$$
Which reworks to:
$$\frac{d^2\phi}{dx^2}+\lambda \phi=0$$
For the latter we also have the boundary conditions:
$$\phi(0)=0\:\text{and }\phi(L)=0$$
The DE for φ(x) is a very simple one of the type we’ve already solved higher up (see e.g. the Pi1DB problem) and the solutions are:
$$\lambda_n=\Big(\frac{n\pi}{L}\Big)^2\:\text{so }\phi_n(x)=A\sin\Big(\frac{n\pi x}{L}\Big)\:\text{for: }n=1,2,3,...$$
The λ<sub>n</sub> are called eigenvalues and the φ<sub>n</sub> eigenfunctions of the DE.
So now we have values for λ (but not for A)!
<hr>
And of course that means we can use these eigenvalues in the DE for h(t):
$$\frac{d^2h}{dt^2}+\Big(\frac{n\pi c}{L}\Big)^2h=0$$
This is a straightforward 2nd order linear DE and its CE has two repeat complex roots and general solution:
$$h(t)=c_1\cos\Big(\frac{n\pi ct}{L}\Big)+c_2\sin\Big(\frac{n\pi ct}{L}\Big)$$
Here we have a useful initial condition:
$$\frac{\partial y(x,0)}{\partial t}=0 \implies \frac{dh(0)}{dt}=0$$
$$\frac{dh}{dt}=-c_1\frac{n\pi c}{L}\sin\Big(\frac{n\pi ct}{L}\Big)+c_2\frac{n\pi c}{L}\cos\Big(\frac{n\pi ct}{L}\Big)$$
$$\frac{dh(0)}{dt}=0 \implies c_2=0$$
So:
$$h(t)=c_1\cos\Big(\frac{n\pi ct}{L}\Big)$$
<hr>
Now remember that we assumed (in German mathspeak: our 'Ansatz'):
$$y(x,t)=\phi(x)h(t)$$
Which gives us a set of solutions:
$$y_n(x,t)=A_n\cos\Big(\frac{n\pi ct}{L}\Big)\sin\Big(\frac{n\pi x}{L}\Big)\:\text{with }A_n=Ac_1$$
$$\text{For: }n=1,2,3,...$$
The Superposition Principle:
To put together a comprehensive solution we need to use the Superposition Principle (SP). There’s nothing new about it and we’ve used the SP
several times before when solving second order linear DEs.
Formally the principle is:
<hr>
$$\text{If }(y_1, y_2,...,y_i,...,y_n)\:\text{are solutions to a linear, homogeneous DE, then }\displaystyle\sum_{i=1}^{n}(c_iy_i)\:\text{,where
}c_i\:\text{are arbitrary constants, is also a solution to the DE.}$$
<hr>
Looking at the expression for y<sub>n</sub>(x,t), for each value of n we have a particular solution of the PDE, so in accordance with the
SP these have to be combined to:
$$y(x,t)=\displaystyle\sum_{n=1}^{\infty}A_n\cos\Big(\frac{n\pi ct}{L}\Big)\sin\Big(\frac{n\pi x}{L}\Big)$$
Scary as it looks, we’ll soon see what it means with some function analysis!
[Edited on 10-6-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Scary ? Terrifying more like !
There's gonna be chain rules everywhere, probably whips and gimp suits too.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | Scary ? Terrifying more like !
There's gonna be chain rules everywhere, probably whips and gimp suits too. |
In fact there's almost nothing we've done here that we haven't seen in action before in the thread.
That's the beauty of Separation of Variables (SoV) of simple PDEs: you don't need to know much more than what's needed for simple ODEs.
The solution of the Schrödinger equation applied to the Hydrogen atom also uses SoV. The assumed solution is then:
$$\psi(r,\theta,\phi)=R(r)Y(\theta,\phi)$$
... with R and Y resp. the radial and angular parts of the wave function.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Erm, are you seriously suggesting that i already have enough knowledge (thanks to you) to be able to compute equations at these
levels of complexity ?
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | | Erm, are you seriously suggesting that i already have enough knowledge (thanks to you) to be able to compute equations at these
levels of complexity ? |
I oppose the Culture of Low Expectations(TM).  
Seriously, that depends on ones level of dedication, of course. At the very least you should be able to follow the derivations presented
here, without too many problems but remember that reading math isn't like reading some flimsy novella. More like reading Shakespeare 'in Ye Olde
English': it takes concentration and some study.
There won't be any exercises on PDEs, just one more example of a simple PDE governing Diffusion. And maybe a chemical example, if I can find a
suitable one...
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Music notes! (Ct'nued)
Frequency spectrum:
The main purpose of a vibrating string is of course to generate sound. The string ‘bangs’ against the air, an elastic medium, and sound waves are
generated. These our ears receive, turn the waves back to oscillations and the resulting electrical impulses are perceived by our brain as sound (here
a music note).
We’ve yet to determine the coefficients A<sub>n</sub>but let’s first look and first time-dependent term in the series, cos(nπct/L).
In wave/oscillation mechanics we write:
$$\cos\Big(\frac{n\pi ct}{L}\Big)=\cos\omega t$$
Where ω is the angular velocity and f the frequency of oscillation:
$$\omega=2\pi f=\frac{n\pi c}{L}$$
$$f=\frac{nc}{2L}$$
$$\frac{T}{\rho}=c^2$$
$$f=\frac{n}{2L}\sqrt{\frac{T}{\rho}}$$
We can see that the vibrating string doesn’t have one single frequency but a frequency spectrum. If for n=1 we call:
$$f_1=\frac{1}{2L}\sqrt{\frac{T}{\rho}}$$
... the fundamental frequency (which defines the note), then the frequency spectrum is:
$$f_1, 2f_1, 3f_1,...$$
... where f<sub>2</sub>, f<sub>3</sub>,... are the so-called harmonics.
Note also:
• Shorter string length gives higher pitch
• Higher string tension gives higher pitch
• Higher density strings give lower pitch
And next we’ll see not all the frequencies are equally represented in the spectrum.
|
|
|
| Pages:
1
..
15
16
17
18
19 |