DubaiAmateurRocketry
National Hazard
   
Posts: 841
Registered: 10-5-2013
Location: LA, CA, USA
Member Is Offline
Mood: In research
|
|
Computational and Theoretical Study of the High Density Energetic Compound HHTDN
Computational and Theoretical Study of the High-Density Energetic Compound HHTDN
(hexanitrohexaazatricyclododecanedinitromethylene)
Introduction.
2,6-Dinitromethylene-1,3,4,5,7,8-HexanitrododecaHydroDIimidazo[4,5-b4',5'-e]pyrazine, hexanitrohexaazatricyclododecanedidinitromethylene, or HHTDN, is
a potential high explosive that came into attention after Xinghui et al's team computed its density to be over 2.1 g/cm3 [1].
This is an extremely high figure considering the density CHON compounds rarely if ever, exceed the 2.1 g/cm3 limit.
The paper claims that the 5-6-5 structure is able to produce highly dense materials, after all, some of the densest compounds in high energy density
materials (HEDM), do in fact contain the 5-6-5 structure. This can be seen in the structure of CL-20 (Hexanitrohexaazaisowurtzitane), as well as
HHTDD(hexanitrohexaazatricyclododecanedione)[2-5].
Figure 1. Structure of CL-20, HHTDD, and HHTDN respectively.
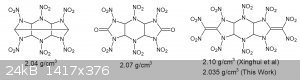
The calculation that obtained the 2.1g/cm3 result was obtained using Politzer's revised equation on predicting crystal densities of CHON
compounds. The equation is highly accurate, with a mean average of 0.03g/cm3 margin error [6]. Notably, many results of Xinghui
et al's calculation was doubtful. For example, their reported calculated heat of formation was exceptionally high, even higher than TTTO's calculated
heat of formation[7]. Not only, their reported density is worth a further investigation.
Therefore a re-computational analysis was performed. Xinghui et al's team used B3LYP at 6-31G(d,p) level, and therefore, I will perform the same run
using the same basis set at the same level. However, this step is already wrong. Xinghui et al's group must have miss-read Politzer's paper when using
B3LYP basis set because Politzer's equation states that the B3PW91 basis set should be used[1],[6]. However, to reproduce the results of a
2.10g/cm3 result, the B3LYP basis set will be used.
To also re-produce the actual theoretical crystal density of HHTDN, an optimization using the B3PW91 will also be performed, which is the actual
method stated on Politzer's paper [6]
Methods.
A list of quantum computational software is used to perform the calculations. The most recent version of ORCA, and Gaussian 09, Multiwfn 3.5, and
Molden is used to perform the analysis of HHTDN[8-11]. As stated above, the optimization run will be using B3LYP at 6-31G(d,p) level to
mimic their methods, while another run using B3PW91 will be performed.
Before this calculation, this method has been used to calculate over 15 existent energetic compounds for calibration and the result was found to be
highly accurate.
Figure 2. HOMO LUMO orbital and ELF of HHTDN
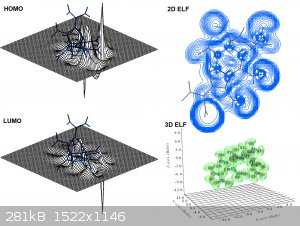
Figure 3. Optimized structure of HHTDN.

Crystal Density.
Using B3LYP, the HOMO LUMO gap and output of HHTDN is relatively acceptable when compared to Xinghui et al's calculations. Multiwfn gave a
sigma2tot value of 394.6kcal/mol2, which is lower than Xinghui et al's calculated value of 445.95. The product of miu
and sigma2tot of 24.747 kcal/mol2, which is also lower than the 49.05 Xinghui calculated. The M/Vm of HHTDN was
2.0760 g/cm3, again, lower than the reported 2.09 g/cm3 from Xinghui et al. In both calculations, B3LYP and B3PW91 gave very
similar sigma2tot and product of miu and sigma2tot values. However, B3PW91 gave a notably higher M/Vm than
B3LYP, at 2.0921 g/cm3. This figure is compatible with what Xinghui et al obtained, however, the B3PW91 produced much lower product of miu
and sigma2tot values which can be seen below in the Multiwfn output image.
Figure 4. Multiwfn output.
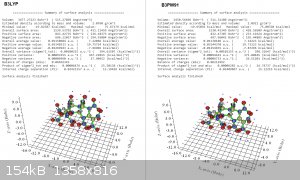
Using politzer's equation:
Crystal density g/cm3= α(M/Vm) + β(vσ2tot)+γ .
The resulting crystal density of HHTDN using B3PW91 is therefore 2.0348/cm3, while the crystal density of HHTDN using B3LYP is calculated
to be 2.0221/cm3. This is evident due to the low sum of miu and sigma2tot of HHTDN produced in both results.
Heat of Formation.
The heat of formation is computed using the PM3 and PM6 method on Gaussian 09. PM3 is used because it has in the past shown to be a relatively
efficient way of obtaining theoretical heat of formation of HEDMs[12], while more recently, PM6 has shown to produce a smaller error margin
than PM3 in 50 compared energetic materials[13]. Due to the higher accuracy fo PM6, its results will be used for further calculations in
detonation performances while PM3 is calculated as a reference.
PM3 calculated heat of formation was obtained to be 588.569 kJ/mol.
PM6 calculated heat of formation was obtained to be 537.578 kJ/mol.
Xinghui et al's heat of formation was reported to be 1330.56 kJ/mol.
Detonation Performances.
Using EMDB as well as the Kamlet-Jacobs equation, an input of C8H4N16O20 as the empirical formula, PM6 output 537.578 kJ/mol as the heat of formation,
and Politzer's equation using optimization form B3PW91 at 6-31G(d,p) level produced 2.0348 g/cm3 as the crystal density, the theoretical
detonation performance was, therefore, obtained 14. The Kamlet-Jacobs equation was chosen due to its popularity and accuracy.
Detonation performance from Kamlet-Jacobs equation:
Km/s = 1.01 (NM1/2Q1/2)1/2 (1+1.30ρ)
GPa = 1.558ρ2NM1/2Q1/2
Xinghui et al:
Heat of formation (kJ/mol) : 1,330
Density (g/cm3) : 2.10
Velocity Det (m/s) : 10,530
Pressure Det (GPa) : 53.70
This work:
Heat of formation (kJ/mol) : 537.58
Density (g/cm3) : 2.035
Detonation Velocity:
K-J Equation (m/s) : 9,524
EMDB1.0 (m/s) : 9,300
Detonation Pressure:
K-J Equation (GPA) : 43.02
EMDB1.0 (GPA) : 43.87
Oxygen balance (Ω): 4.97
Detonation Temp (K): 5251
Summary
In summary, the detonation performance of HHTDN, at 9,524m/s and 42GPa is rather high, but rather low compared to the 10,530 m/s Xinghui et al has
calculated. Since theoretical and computational chemistry is meant to guide chemists to synthesize the most promising molecules, I hope this
calculation have saved one's some time if one ever hoped to synthesize the HHTDN that would have almost broke the performance limit of CHON materials
[15].
As for what could have went wrong for Xinghui et al's calculations, the PM6 output on HHTDN, the RPM6 output was 0.204752 Hartree, the enthalpy (which
has nothing to do with enthalpy), gave a value of 0.49 Hartree, which translates to 1,310kJ, is strikingly similar to the number Xinghui et al
reported. However Xinghui et al's team did not calculate using PM3 or PM6 methods, therefore it is unclear what has gone wrong in their calculations.
As for the differences in optimization, I am more confident in my results because over 15 existent compounds have been calculated in the past, and
when compared to experimental calculated crystal density, was found to be highly accurate.
Reference:
[1] Jin, Xinghui, et al. "Molecule and Synthesis Design of a Family of High Energy Density Materials Based on “565” Chemical Structure."
ChemistrySelect 3.4 (2018): 1142-1150.
[2] Duda, Aleksandra. Synthesis of hexanitrohexaazatricyclododecanedione (HHTDD). Diss. Zakład Materiałów Wysokoenergetycznych, 2016.
[3] LIU, Yu-zhu, Zhi-yu YU, and Jiang-yong YU. "Piperazine Chemistry Part Ⅰ Developments on Synthesis of High Energy Density Compound of Piperazine
Series [J]." Chinese Journal of Energetic Materials 3 (2008): 028.
[4] Simpson, R. L., et al. "CL‐20 Performance Exceeds that of HMX and its Sensitivity is Moderate." Propellants, Explosives, Pyrotechnics 22.5
(1997): 249-255.
[5] Hoffman, D. Mark. "Voids and Density Distributions in 2, 4, 6, 8, 10, 12‐Hexanitro‐2, 4, 6, 8, 10, 12‐Hexaazaisowurtzitane (CL‐20)
Prepared Under Various Conditions." Propellants, Explosives, Pyrotechnics: An International Journal Dealing with Scientific and Technological Aspects
of Energetic Materials 28.4 (2003): 194-200.
[6] Politzer, Peter, et al. "An electrostatic correction for improved crystal density predictions of energetic ionic compounds." Molecular Physics
108.10 (2010): 1391-1396.
[7] Politzer, Peter, Pat Lane, and Jane S. Murray. "Computational characterization of two di-1, 2, 3, 4-tetrazine tetraoxides, DTTO and iso-DTTO, as
potential energetic compounds." Central European Journal of Energetic Materials 10.1 (2013).
[8] Neese, Frank. "The ORCA program system." Wiley Interdisciplinary Reviews: Computational Molecular Science 2.1 (2012): 73-78.
[9] Frisch, M. J. E. A., et al. "Gaussian 09, revision a. 02, gaussian." Inc., Wallingford, CT 200 (2009).
[10] Schaftenaar, Gijs, and Jan H. Noordik. "Molden: a pre-and post-processing program for molecular and electronic structures." Journal of
computer-aided molecular design 14.2 (2000): 123-134.
[11] Lu, Tian, and Feiwu Chen. "Multiwfn: a multifunctional wavefunction analyzer." Journal of computational chemistry 33.5 (2012): 580-592.
[12] De Paz, Jose‐Luis G., and Juan Ciller. "On the Use of AMl and PM3 Methods on Energetic Compounds." Propellants, explosives, pyrotechnics 18.1
(1993): 33-40.
[13] Gong, C. Z., X. L. Zeng, and X. H. Ju. "Comparative PM6 and PM3 study on heats of formation for high energetic materials." Computers and applied
chemistry 31.4 (2014): 445-450.
[14] Kamlet, Mortimer J., and S. J. Jacobs. "Chemistry of detonations. I. A simple method for calculating detonation properties of C–H–N–O
explosives." The Journal of Chemical Physics 48.1 (1968): 23-35.
[15] Pepekin, V. I., and S. A. Gubin. "Propellant performance of organic explosives and their energy output and detonation velocity limits."
Combustion, Explosion, and Shock Waves 43.1 (2007): 84-95.
Final Edit: July 27th 2018.
[Edited on 27-7-2018 by DubaiAmateurRocketry]
[Edited on 27-7-2018 by DubaiAmateurRocketry]
|
|
|
DubaiAmateurRocketry
National Hazard
   
Posts: 841
Registered: 10-5-2013
Location: LA, CA, USA
Member Is Offline
Mood: In research
|
|
Updated calculation on the condensed heat of formation from the heat of formation sublimation adopted by byrd and rice et al.
Eq 1.
Heat of Formation(Condensed) = Heat of formation(Gas)- 2Heat of formation(Sub).
Eq 2.
Heat of Formation(Sub) = 2.67*10-4Ås2 + 1.650(vσ2tot)0.5 + 2.966
Ås is the surface area.
(vσ2tot) is the a summary of positive and
negative variances of their surface electrostatic potentials. This is an effective
measure of a molecule’s tendency for non-covalent interactions
_______
Calculation:
0.000267*(428^2)+(1.65*(24.7)^0.5)+2.96 = 60.0kcal
60.0kcal = 251 kJ
588kJ -251 kJ = 337 kJ
_______
The new heat of formation plugged into K-J equation produces an 80 m/s loss in detonation velocity compared to above.
[Edited on 6-8-2018 by DubaiAmateurRocketry]
|
|
|
|