quantumchromodynamics
Hazard to Self
 
Posts: 67
Registered: 25-9-2013
Location: with much determination, nowhere in particluar
Member Is Offline
Mood: tired but still trying
|
|
atomic model
In college I took the chemistry necessary for my engineering degree. Many years later, as I am studying chemistry for myself, the atomic model is
fascinating. Before, I just memorized the pictures and shapes and fill orders and passed the tests and forgot. Now I am personally invested and want
to understand what I can.
Ignoring neutrons, to makeup the next element, a proton and an electron are added to the previous element. The proton goes into the nucleus. What
happens inside the nucleus is utterly mysterious. The added electron either completes an existing suborbital, or starts the next lowest energy
suborbital. An electron pair is needed to complete a suborbital.
The diagrams of suborbitals represent a possible quantum vibration (probability wave function).
For simplicity let us limit discussion to just the first and second shell and the S orbital.
The S orbital is spherical in shape with a probability density that increases inwards towards the center.
My first question is this.
Does the probability density of the S orbital extend outwards to infinity, or is there a boundary condition? If there is no boundary then is there
some probability of finding an electron from the 1S orbital inside the 2S orbital, or even the 3F orbital?
What keeps electrons constrained to a shell?
My second question is sort of my first question inverted:
Is the probability density of the S orbital highest at the center? Does the center coincide with the nucleus, or is there some inner boundary? If
there is no boundary condition, does this mean there some probability of finding an electron from the 1S orbital inside the nucleus?
What keeps electrons out of the nucleus?

|
|
|
sonogashira
National Hazard
   
Posts: 555
Registered: 10-9-2006
Member Is Offline
Mood: No Mood
|
|
I was recommended this book by a gentle man on this forum:
http://luizfernando.info/pbd/The%20Case%20Against%20The%20Nu...
It looks like an interesting read, although I have yet to do more than have a brief read of passages; but perhaps you will find it interesting, yet
not at all helpful in answering your questions! For which, perhaps a physical chemistry text book would be most suitable, yet I am afraid that I do
not know of a single textbook on physical chemistry worth recommending.  Regardless, I would suggest that questions of 'what is the case', rather than 'why is the case the case', would be more-likely to yield acceptable
answers, since theories change, yet-- according to one theory(!)-- the facts do not!
Regardless, I would suggest that questions of 'what is the case', rather than 'why is the case the case', would be more-likely to yield acceptable
answers, since theories change, yet-- according to one theory(!)-- the facts do not!
As far as I know:
Electron-capture by the nucleus is assumed, and used to explain common nuclear reactions; the probability of an electron being at the nucleus rapidly
trends towards zero, however, although I'm not sure how this discrepancy is explained, save for the use of a different mathematical template, which
suggests both the cause, and solution, to the 'discrepency' in the first-place! 
|
|
|
DJF90
International Hazard
    
Posts: 2266
Registered: 15-12-2007
Location: At the bench
Member Is Offline
Mood: No Mood
|
|
I guess the simplest way to find the answers would be to consider the wavefuction. We know that the probability of finding an electron at a radius of
x and y from the nucleus is the integral of psi*psi between y and x.
Considering your first queston... The probability of finding the electron at an infinite distance. We'll say value Y is ∞, and we'll say that X
is ∞ minus an infinitesimal amout. We can approximate that X therefore is also ∞. It then follows that the integral is zero.
Your second question is more difficult. The maximum probability density is not at the centre of the nucleus. As you move closer to the nucleus, there
is the issue of electron electron repulsion increasing as the orbital is being made less diffuse. This is where the radial distribution function comes
in. See this site for details http://winter.group.shef.ac.uk/orbitron/AOs/1s/radial-dist.h...
If you change the orbital using the left hand menu, then you'll need to select the radial distribution tab at the top of the page.
|
|
|
phlogiston
International Hazard
    
Posts: 1375
Registered: 26-4-2008
Location: Neon Thorium Erbium Lanthanum Neodymium Sulphur
Member Is Offline
Mood: pyrophoric
|
|
Quote: Originally posted by quantumchromodynamics  | | Does the probability density of the S orbital extend outwards to infinity, or is there a boundary condition? If there is no boundary then is there
some probability of finding an electron from the 1S orbital inside the 2S orbital, or even the 3F orbital? |
There is no boundary. It goes to zero only -at- infinity, but in all finite space, its value is never zero. There is a very small chance you can
detect that electron in the next room, on the moon, on alpha centauri, etc. Certainly also inside the 2S orbital or any other orbital.
| Quote: | | What keeps electrons constrained to a shell? |
The electrostatic force mostly, and the pauli exclusion principle.
My second question is sort of my first question inverted:
| Quote: | | Is the probability density of the S orbital highest at the center? Does the center coincide with the nucleus, or is there some inner boundary? If
there is no boundary condition, does this mean there some probability of finding an electron from the 1S orbital inside the nucleus?
|
In all text books I have ever read the 1S orbital was calculated on the basis of the electrostatic interaction with the nucleus alone. I am not sure
if the weak force may play a role here, changing the wavefunction near/inside the nucleus. Ignoring that, the probability density is then highest at
the nucleus/the center, and then possibility of finding the electron inside the volume of the nucleus is not zero.
-----
"If a rocket goes up, who cares where it comes down, that's not my concern said Wernher von Braun" - Tom Lehrer |
|
|
turd
National Hazard
   
Posts: 800
Registered: 5-3-2006
Member Is Offline
Mood: No Mood
|
|
phlogiston is right, DJF90 and sonogashira are wrong: electron density at the nucleus is distinctly non-zero.
Stop confusing the probability density and the radial probability density. The webpage linked to above even says:
| Quote: | | For s-orbitals, the radial distribution function is given by multiplying the electron density by 4πr<sup>2</sup>
|
So whatever the probability density is at r=0, the radial probability density will always be 0, because you are comparing the total density of a
sphere (r=/=0) with that of a point (r=0). Of course the latter is 0.
PS: This has been discussed ad nauseam. UTFSE.
[Edited on 5-10-2013 by turd]
|
|
|
sonogashira
National Hazard
   
Posts: 555
Registered: 10-9-2006
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by turd  |
Stop confusing the probability density and the radial probability density. The webpage linked to above even says:
| Quote: | | For s-orbitals, the radial distribution function is given by multiplying the electron density by 4πr<sup>2</sup>
|
[Edited on 5-10-2013 by turd] |
You've confused the radial probability DISTRIBUTION with the radial probability density. They're not the same thing. UTFSE. 
|
|
|
arsphenamine
Hazard to Others
  
Posts: 236
Registered: 12-8-2010
Location: I smell horses, Maryland, USA
Member Is Offline
Mood: No Mood
|
|
The computational chem folks use a probability density value of .002 as a cutoff point for electron orbitals/clouds/soup since it corresponds well to
Van der Waals radii. The generated molecular shape/surface/volume is more detailed than a bulk VdW sphere and allows more insight from molecular
docking simulations.
The .002 density 'boundary' can be calculated from both ab initio and semi-empirical methods for most molecular environments, so sophisticated
solvation models use these isosurfaces instead of empirical Van der Waals radius values.
[edit]
The assertion that electron probability <mumble-type> extends to infinity is mathematically important but not chemically germane, more akin to
asking how many angels can sit on the head of a pin.
Measure the angels' arses, measure the head of a pin, calculate surface areas for both, then divide the latter by the former. The numerical result is
left as an exercise for pedants.
[Edited on 5-10-2013 by arsphenamine]
|
|
|
turd
National Hazard
   
Posts: 800
Registered: 5-3-2006
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by sonogashira  | You've confused the radial probability DISTRIBUTION with the radial probability density. They're not the same thing. UTFSE.  |
Why do you think so? The "radial probability distribution" certainly is a probability density function.
Since electrons do not have a discrete position, it's all about densities.
And what do you mean with "radial probability DISTRIBUTION" anyway? Do you maybe believe that it's the cumulative radial distribution function (p(x):
probability to find the electron at r<x)? For this you would have to multiply with a factor in r3, not r2.
And in any case it doesn't change the fact that phlogiston was right and you were wrong.
[Edited on 5-10-2013 by turd]
|
|
|
sonogashira
National Hazard
   
Posts: 555
Registered: 10-9-2006
Member Is Offline
Mood: No Mood
|
|
I was wrong about what?
|
|
|
turd
National Hazard
   
Posts: 800
Registered: 5-3-2006
Member Is Offline
Mood: No Mood
|
|
Take an infinitesimal volume element -> the probability to find an electron in there increases as you approach the nucleus.
As I said, this has been discussed ad nauseam on this board...
|
|
|
sonogashira
National Hazard
   
Posts: 555
Registered: 10-9-2006
Member Is Offline
Mood: No Mood
|
|
I see a rapid trend towards zero (http://www.dartmouth.edu/~genchem/0405/spring/6belbruno/radi...); but as you will.
|
|
|
turd
National Hazard
   
Posts: 800
Registered: 5-3-2006
Member Is Offline
Mood: No Mood
|
|
*sigh*
You haven't understood what the radial probability distribution is. 
The probability density of the 1s electron of an isolated H radical is something like A*exp(-r*B)1, where r is the distance from the
nucleus and A and B are two positive constants. You will agree that the density is anisotropic and that the highest density is located at the nucleus.
To get the radial probability distribution, you integrate over the surface of a sphere with radius r and centre at the nucleus. Of course this is zero
at the nucleus, because the corresponding sphere has no surface.
Read this: https://en.wikipedia.org/wiki/Atomic_orbital
| Quote: | | The s-orbitals for all n numbers are the only orbitals with an anti-node (a region of high wave function density) at the center of the nucleus.
|
(The probability density is proportional to the square of the wave function)
1 Of course strongly simplified.
PS: I'm not a theoretician and don't even play one on TV, but this is elementary math...
|
|
|
sonogashira
National Hazard
   
Posts: 555
Registered: 10-9-2006
Member Is Offline
Mood: No Mood
|
|
http://www.chem1.com/acad/webtut/atomic/WhyTheElectron.html
|
|
|
turd
National Hazard
   
Posts: 800
Registered: 5-3-2006
Member Is Offline
Mood: No Mood
|
|
So? This is saying the same thing that I'm saying all the time.
Just look at this picture:
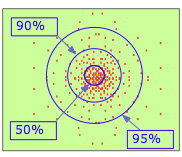
Where is the highest probabiity to find an electron? Bingo - at the nucleus.
A radial probability density function is by definition always zero at the origin, whether you put the origin at the nucleus or somewhere
completely different. Therefore it can never tell us where there is the highest probability to find an electron.
Is multiplication with zero really such a difficult concept for you?
The wave functions of the nucleus and the s-electrons penetrate. These are not billard balls. Get over it.
PS: The last paragraph in the article shows that the author has some conceptual issues. It's tautological. Compare the density of a point with that of
a finite surface, the first is zero.
|
|
|
sonogashira
National Hazard
   
Posts: 555
Registered: 10-9-2006
Member Is Offline
Mood: No Mood
|
|
Believe what you like.
|
|
|
maxpayne
Hazard to Self
 
Posts: 78
Registered: 15-11-2011
Member Is Offline
Mood: No Mood
|
|
One must understand that current atom theory is still only a theory.
Leading scientists, in many documentaries I watched, are saying that current theory is the best model they have, never claiming that is 100% correct.
Probability is high that is correct, but this does not prove it, and what is more important in my opinion, is that no one should believe anything they
don't want to.
However, one must first learn what is offered in mainstream physics, since it can open many doors to research he's own understanding. It is just a
mathematical model continuously researched and patched. This patching is what makes this model attracting. I strongly believe that all the experiments
done to prove atom theory are highly valuable and nothing will ever be lost if theory is changed since all the data is gathered and saved that could
test any upcoming theory and this is real value.
The main question is: Does atom exists at all and if it exists, is math able to describe the nature?
I could continue and make this post really big, but who cares what I think, since currently I can't offer anything new to be an alternative to current
theory, so I'll stop here with some quotes.
"Today's scientists have substituted mathematics for experiments, and they wander off through equation after equation, and eventually build a
structure which has no relation to reality."
Nikola Tesla, Modern Mechanics and Inventions, July, 1934
"Searching for a smallest particle of matter, man found an atom, consisting of never ending smaller particles."
Anonymous
|
|
|
quantumchromodynamics
Hazard to Self
 
Posts: 67
Registered: 25-9-2013
Location: with much determination, nowhere in particluar
Member Is Offline
Mood: tired but still trying
|
|
many thanks
I now have days of highly interesting study ahead of me. Many thanks to all who provided insight or opinion.
DJF90: Amazing, beautiful, insightful...
MAXPAYNE: Tesla was right. Math is great, but the education of mind and intuition through experiment makes it real.
|
|
|