| Pages:
1
..
31
32
33
34
35
..
76 |
greenlight
National Hazard
   
Posts: 705
Registered: 3-11-2014
Member Is Offline
Mood: Energetic
|
|
Very nice purple on the zipper reaction!
I purchased the powder dyes online and it did not specify on the listing or the packaging what type of exact dye they were.
I am fairly sure the yellow is solvent yellow 33 dye and the blue could be solvent blue dye 35 or 36.
|
|
|
DFliyerz
Hazard to Others
  
Posts: 241
Registered: 22-12-2014
Member Is Offline
Mood: No Mood
|
|
Some interesting crystals when I was decarboxylating salicylic acid to phenol, and an odd precipitate in my wash/waste bin (I think it may have been
in part from the reaction of sucrose, sodium hydroxide, and copper sulfate, but the strange lumps on the bottom and lack of Rochelle's salt say
otherwise.)
https://feen.us/k396.jpg
https://feen.us/4af1.jpg
(Too large to embed!)
[Edited on 6-5-2015 by DFliyerz]
|
|
|
Zephyr
Hazard to Others
  
Posts: 341
Registered: 30-8-2013
Location: Seattle, WA
Member Is Offline
|
|
Wow, interesting crystals!
Maybe the orangish red precipitate is copper (I) oxide?
|
|
|
The Volatile Chemist
International Hazard
    
Posts: 1981
Registered: 22-3-2014
Location: 'Stil' in the lab...
Member Is Offline
Mood: Copious
|
|
Cool! The Zipper reaction looks great. Like to try it sometime.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
And so you shall TVC !
|
|
|
The Volatile Chemist
International Hazard
    
Posts: 1981
Registered: 22-3-2014
Location: 'Stil' in the lab...
Member Is Offline
Mood: Copious
|
|
What? Oh, is it common in college or something? Definitely looking forward to AP Chem & AP Bio and Calc AB next year (Junior in HS).
|
|
|
Brain&Force
Hazard to Lanthanides
    
Posts: 1302
Registered: 13-11-2013
Location: UW-Madison
Member Is Offline
Mood: Incommensurately modulated
|
|
Back on track guys
<blockquote class="twitter-tweet" lang="en"><p lang="da" dir="ltr">Lanthanides, part 2: dysprosium and ytterbium <a
href="https://twitter.com/hashtag/realtimechem?src=hash">#realtimechem</a> <a
href="http://t.co/VyyFL8OIW7">pic.twitter.com/VyyFL8OIW7</a></p>— Brain&Force (@brainandforce) <a
href="https://twitter.com/brainandforce/status/608061459373948928">June 9, 2015</a></blockquote> <script async
src="//platform.twitter.com/widgets.js" charset="utf-8"></script>
At the end of the day, simulating atoms doesn't beat working with the real things...
|
|
|
mayko
International Hazard
    
Posts: 1218
Registered: 17-1-2013
Location: Carrboro, NC
Member Is Offline
Mood: anomalous (Euclid class)
|
|
I made some iodoform recently, and recrystallized half of it from alcohol. The other half I tried to dry crude, and the base remaining on it appears
to have caused it to decompose and release iodine - the filter paper and jar were stained brown. Now, though, there are these lovely formations
growing on the lye I was using as a desicant!
Here's the conifer gall of a Gymnosporangium juniperi-virginianae . This fungus spends half its life cycle on apple trees, and the other half on junipers.
al-khemie is not a terrorist organization
"Chemicals, chemicals... I need chemicals!" - George Hayduke
"Wubbalubba dub-dub!" - Rick Sanchez
|
|
|
DFliyerz
Hazard to Others
  
Posts: 241
Registered: 22-12-2014
Member Is Offline
Mood: No Mood
|
|
I was kind of thinking that too, but the color of the clumps and the chemicals in there don't really match.
|
|
|
PHILOU Zrealone
International Hazard
    
Posts: 2893
Registered: 20-5-2002
Location: Brussel
Member Is Offline
Mood: Bis-diazo-dinitro-hydroquinonic
|
|
@Mayko,
Isn't iodoform yellow?
PH Z (PHILOU Zrealone)
"Physic is all what never works; Chemistry is all what stinks and explodes!"-"Life that deadly disease, sexually transmitted."(W.Allen)
|
|
|
DraconicAcid
International Hazard
    
Posts: 4278
Registered: 1-2-2013
Location: The tiniest college campus ever....
Member Is Offline
Mood: Semi-victorious.
|
|
Yes, but if it's contaminated with iodine, it would probably have that icky brown colour.
Please remember: "Filtrate" is not a verb.
Write up your lab reports the way your instructor wants them, not the way your ex-instructor wants them.
|
|
|
mayko
International Hazard
    
Posts: 1218
Registered: 17-1-2013
Location: Carrboro, NC
Member Is Offline
Mood: anomalous (Euclid class)
|
|
Yes - and that's a picture of the NaOH I was using as a desiccant; sorry if I was unclear.
al-khemie is not a terrorist organization
"Chemicals, chemicals... I need chemicals!" - George Hayduke
"Wubbalubba dub-dub!" - Rick Sanchez
|
|
|
The Volatile Chemist
International Hazard
    
Posts: 1981
Registered: 22-3-2014
Location: 'Stil' in the lab...
Member Is Offline
Mood: Copious
|
|
Nice photos. What method did you use to produce the iodoform? (And, just curious, what does iodoform smell like?)
|
|
|
pneumatician
Hazard to Others
  
Posts: 409
Registered: 27-5-2013
Location: Magonia
Member Is Offline
Mood: ■■■■■■■■■■ INRI ■■■■■■■■■■ ** Igne Natura Renovatur Integra **
|
|
extract from flowers.

|
|
|
PHILOU Zrealone
International Hazard
    
Posts: 2893
Registered: 20-5-2002
Location: Brussel
Member Is Offline
Mood: Bis-diazo-dinitro-hydroquinonic
|
|
What was your process for CHI3?
I2 is soluble in brown in ethanol.
--> Was your recrystallization solvent orange-brown?
In a little chloroform I2 colours the solution in violet-purple.
That would prove some I2 formation.
If some of the NaOH has decomposed the iodoform or an intermediary compouns into I(-)...then NaI complexes iodine as brown-orange NaI3.
Alternatively ethanol may be oxydised by iodine into ethanal (what is subject to iodoform reaction)...ethanal will polymerize into orange-Brown tarry
material upon exposure to strong base like lye (NaOH).
PH Z (PHILOU Zrealone)
"Physic is all what never works; Chemistry is all what stinks and explodes!"-"Life that deadly disease, sexually transmitted."(W.Allen)
|
|
|
Brain&Force
Hazard to Lanthanides
    
Posts: 1302
Registered: 13-11-2013
Location: UW-Madison
Member Is Offline
Mood: Incommensurately modulated
|
|
<a title="By brainandforce (Own work) [CC0], via Wikimedia Commons" href="https://commons.wikimedia.org/wiki/File%3AHolmium_shards.jpg"><img
width="512" alt="Holmium shards" src="//upload.wikimedia.org/wikipedia/commons/thumb/3/38/Holmium_shards.jpg/512px-Holmium_shards.jpg" width=800
/></a>
I uploaded my first image to Wikimedia Commons, these are holmium shards.
[Edited on 12.6.2015 by Brain&Force]
At the end of the day, simulating atoms doesn't beat working with the real things...
|
|
|
alexleyenda
Hazard to Others
  
Posts: 277
Registered: 17-12-2013
Location: Québec, Canada
Member Is Offline
Mood: Busy studying chemistry at the University
|
|
Some pretty *disgusting* pictures, an extraction after a pdc oxydation (pyridinium dichromate). This reaction is such a pain in the @ to clean. And
that is before I tried to wash it. It became worst when I started rubbing it with a brush, the crap stretched accross the glassware -_-
 
[Edited on 12-6-2015 by alexleyenda]
Help us build the Sciencemadness Wiki! Every question and tips about amateur chemistry two clicks away, wouldn't that be awesome?!
sciencemadness.org/smwiki
|
|
|
The Volatile Chemist
International Hazard
    
Posts: 1981
Registered: 22-3-2014
Location: 'Stil' in the lab...
Member Is Offline
Mood: Copious
|
|
Nice! What procedure was used?
What's the gunk made of? Is it the product, or chromium junk?
|
|
|
plastics
Hazard to Others
  
Posts: 141
Registered: 6-11-2009
Member Is Offline
Mood: No Mood
|
|
Sodium salt of 1-hydroxy-2-naphthoyl-o-benzoic acid
Precursor to series of fluorescent dyes
Looks just like liquid gold
When dissolved in water gives deep olive-green solution
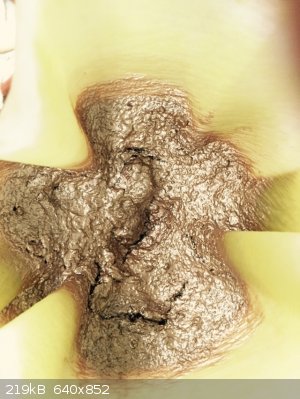
|
|
|
DutchChemistryBox
Hazard to Self
 
Posts: 74
Registered: 24-3-2013
Location: Strasbourg
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by plastics  | Sodium salt of 1-hydroxy-2-naphthoyl-o-benzoic acid
Precursor to series of fluorescent dyes
Looks just like liquid gold
When dissolved in water gives deep olive-green solution |
Interresting! What are you going to make?
|
|
|
pyro2525
Harmless

Posts: 5
Registered: 17-4-2015
Member Is Offline
Mood: No Mood
|
|
Manganese (II) Chloride, recrystallization test sample out of batch.
It is such a deliquescent bitch, redissolving whenever it rained. This came out of about a week in a desiccant bag.
The single crystals at the beginning were much prettier but I didn't want to risk taking it out.

|
|
|
mayko
International Hazard
    
Posts: 1218
Registered: 17-1-2013
Location: Carrboro, NC
Member Is Offline
Mood: anomalous (Euclid class)
|
|
| Quote: |
(And, just curious, what does iodoform smell like?)
|
A little like chloroform, but maybe more astringent. During preparation, there is a much stronger smell, a nauseating, cloying sweet smell, dissimilar
to chloroform; this smell seems to remain with the aqueous layer.
| Quote: |
What was your process for CHI3?
|
I dissolved iodine in acetone and added sodium hydroxide solution.
| Quote: |
I2 is soluble in brown in ethanol.
--> Was your recrystallization solvent orange-brown?
|
It was a deep orange-yellow, but not so strong I suspected leftover iodine. The decomposition was striking: I put both samples into desiccators, the
crude stuff as lumps, the pure stuff as crystals. They appeared identical colors. A day later, the crystals were fine; the lumps had turned a dark
brown, almost black, which had stained the filter paper holding them.
Chloroform is reactive with base (I had vague memories of this being important when making it from bleach and acetone; the product is to be
removed in a timely manner otherwise it will decay) but it isn't clear how a base would convert a haloform to a halogen.
al-khemie is not a terrorist organization
"Chemicals, chemicals... I need chemicals!" - George Hayduke
"Wubbalubba dub-dub!" - Rick Sanchez
|
|
|
Zephyr
Hazard to Others
  
Posts: 341
Registered: 30-8-2013
Location: Seattle, WA
Member Is Offline
|
|
I like those crystals pyro!
Here are a few of my own, these are vanillic acid being recrystallized:
Remnants:

And the final drying crystals:

|
|
|
The Volatile Chemist
International Hazard
    
Posts: 1981
Registered: 22-3-2014
Location: 'Stil' in the lab...
Member Is Offline
Mood: Copious
|
|
"deliquescent bitch"
Lol, would make a BA band name, or a great pompous curse word to use on certain foul womenfolk 
|
|
|
alexleyenda
Hazard to Others
  
Posts: 277
Registered: 17-12-2013
Location: Québec, Canada
Member Is Offline
Mood: Busy studying chemistry at the University
|
|
The procedure could not be more simple, PDC with the molecule to oxidize in a solvent, the junk is probably chromium junk.
Help us build the Sciencemadness Wiki! Every question and tips about amateur chemistry two clicks away, wouldn't that be awesome?!
sciencemadness.org/smwiki
|
|
|
| Pages:
1
..
31
32
33
34
35
..
76 |