| Pages:
1
2
3
4
..
33 |
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
A mini math-excursion: Complex Numbers
Complex numbers play a big part in QM/WM (although much less in its chemical applications, so we’ll keep it to a bare minimum). But since as
you’ll see the symbol “i” frequently in the QM context, it’s worth to briefly elaborate. You might learn something, like a
Xmas party trick or somefink.
At the heart of complex numbers lays the imaginary number i (“eye”):
i = √(-1) (the Square Root of minus one)
The ‘imaginary’ number i is not a Real Number because square roots of negative number have no (Real) roots. But the square of i, that is
i<sup>2</sup> = - 1, IS real (but negative). Complex Numbers can thus be used in calculations, sometimes yielding other CNs, sometimes
yielding Real Numbers.
A general Complex Number takes on the format:
z = x + yi with x the Real part and yi the Imaginary (or complex) part, the choice of symbols x
and y is entirely arbitrary and up to the author.
The conjugated complex number of z, denoted as z<sup>*</sup> (“zed starred”) is:
z<sup>*</sup> = x – yi
So the conjugated complex number is obtained by inverting the sign of the complex part of the complex number (+ to – or – to +)
Via Euler, Complex Numbers are often expressed in their exponential form:
z = r e<sup>θi</sup> and its complex conjugate z<sup>*</sup> = r e<sup>-θi</sup>
or z = r cosθ + r sinθ i (or z = r cosθ + (r sinθ) i , to be perhaps clearer, as the sine acts on θ but not i)
Trigonometry then establishes the relation between (r,θ) and (x,y): x = r cosθ, y = r sinθ
Consequence for QM/WM:
An important property of Complex Numbers (CNs) and their complex conjugates is that the product of a CN and its complex conjugate is a Real Number and
positive, always:
(meaning z<sup>*</sup> times z) z<sup>*</sup>z = r e<sup>θi</sup> r e<sup>-θi</sup> =
r<sup>2</sup> e<sup> θi – θi</sup> = r<sup>2</sup> e<sup>0</sup> = r<sup>2</sup>
In QM/WM this has an important application because the product of the wave function ψ (soon to be discussed, for all you hunky learners!) and its
complex conjugate ψ<sup>*</sup> , that is ψ<sup>*</sup>ψ is always a Real Number.
Ψ(x)<sup>*</sup>ψ(x) is related to the probability of finding the particle at location x and probability (P) is always
a Real and Positive Number.
Numerical Example: c = 5 - 3i, thus c<sup>*</sup> = 5 + 3i
c<sup>*</sup>c = (5 - 3i)(5 + 3i)
= 25 + 15i – 15i – 9i<sup>2</sup>
= 25 – 9 (-1)
= 25 + 9
= 34
Or for a general CN like c = x +/- yi,
c<sup>*</sup>c = x<sup>2</sup> + y<sup>2</sup>
And that’s it for this one, folks (you beautiful people  ). Please, send
us your questions, comments, corrections, magical incantations or moneys… ). Please, send
us your questions, comments, corrections, magical incantations or moneys…
[Edited on 10-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
That is the best and most concise explanation of i that I have ever heard or read.
Thanks bloggers.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
It's only the tip of a Complex Iceberg!
|
|
|
annaandherdad
Hazard to Others
  
Posts: 387
Registered: 17-9-2011
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by Magpie  |
I found the explanation for the shape of the black body radiation curve vs temperature to be the most astounding. This explains how the color of a
heated metal indicates its temperature. Was it de Broglie or was it Planck that discovered this?
|
A bit of history. In the 1870's Boltzmann applied classical thermodynamics, itself a relatively new development (Kelvin, Clausius et al, 1850's) to
the problem of black body radiation. By doing a gedankenexperiment in which black body radiation was the working fluid in a Carnot cycle, he showed
that the total energy in a given volume of black body radiation is proportional to T^4. The same had been observed experimentally by Stefan, and is
now known as the Stefan-Boltzmann law; Stefan's experimental results gave a numerical value for the constant of proportionality. Boltzmann just used
some simple thermodynamics, plus a bit of electromagnetic theory, the latter needed to show that the pressure is 1/3 of the energy density. The
argument is simple and beautiful, and easily understood by a physics undergraduate today.
After this the main problem was to determine how the energy in black body radiation is distributed over frequency. Important advances were made by
Wien, who by the early 1890's had derived his displacement law, which shows how the power spectrum of radiation scales with temperature, and his
approximation to the power spectrum itself, which is accurate at high frequencies. Wien's arguments, unlike Boltzmann's, are somewhat complicated and
not as interesting from a modern standpoint, but they represented real progress. In particular, Wien's high temperature formula shows the power
spectrum (ie, the energy per unit frequency per unit volume in BB radiation) involves the quantity exp(-h*nu/k*T), where nu is the frequency, k is
Boltzmann's constant and h is a new constant that we now call Planck's constant. This was the first appearance of Planck's constant in physics.
Although Planck did not discover this constant, he did recognize that this was a new, fundamental constant of nature, on an equal footing with the
speed of light, the charge on the electron, and Newton's constant of gravitation. Indeed, Planck realized that using this fundamental constant and
the others one could construct a fundamental unit of length, time, energy, mass etc, units that are now called Planck units (the Planck length is
about 10^{-33} cm, and it is the length scale at which the effects of both gravity and quantum mechanics are expected to appear). This was all before
the correct distribution law was discovered.
A different theoretical argument, based on classical thermodynamics and a mode decomposition of the electromagnetic field, yields the Raleigh-Jeans
law, which is valid at low frequencies, but which diverges at high frequencies. This divergence is called an "ultraviolet catastrophe".
Planck devoted himself to working out the formula for the power spectrum of BB radiation in the early 1890's, and worked on it for several years. His
efforts focused on using electromagnetic theory to model the exchange of energy between matter and electromagnetic radiation. He worked with a
kinetic equation describing the statistical flow of energy between matter and field, and attempted to find the equilibrium solution by a version of
Boltzmann's "H-theorem", which was known to work for finding the equilibrium distribution of velocities in an ideal gas. Initially, Planck rejected
Boltzmann 's statistical arguments, and had some sharp and public disagreements with him. Over time, however, Planck slowly began to realize that
Boltzmann was right about statistics. This was a time in which the modern theory of equilibrium statistical mechanics was barely known (it had been
developed recently by Gibbs, an American who wrote a book in English on his work. Gibb's work seems not to have been known to Planck). Later, in
1906, after Boltzmann had committed suicide, Planck expressed some regret and remorse, in a kind of acknowledgement of how much he owed to Boltzmann.
The breakthrough came in the fall of 1899, when Rubens and other experimentalists got some data on the low frequency end of the spectrum. Planck used
this to interpolate between two formulas he had been playing with for the entropy of the BB radiation, and obtained the now-accepted formula for the
power spectrum, which agreed with the experimental data.
Planck was lucky that he was in Berlin at the time, which is where the experimental work was going on. I wish I knew more about how Rubens and the
others did it; I believe they developed effective bolometers, and I suspect that they used electric ovens to create the BB radiation.
The problem then was to justify the formula. In two months of furious work Planck did so, based on an ad hoc assumption that the exchange of energy
between mechanical oscillators and the field could only take place in units of h*nu. The formula and the derivation were announced in December, 1899.
The story of how the wave-particle duality was discovered proceeds from this point. The main ideas were supplied by Einstein.
[Edited on 11-7-2015 by annaandherdad]
Any other SF Bay chemists?
|
|
|
The Volatile Chemist
International Hazard
    
Posts: 1981
Registered: 22-3-2014
Location: 'Stil' in the lab...
Member Is Offline
Mood: Copious
|
|
Great idea! Enjoying the explanation so far! May implement the key points into a program of some kind.
|
|
|
Polverone
Now celebrating 21 years of madness
        
Posts: 3186
Registered: 19-5-2002
Location: The Sunny Pacific Northwest
Member Is Offline
Mood: Waiting for spring
|
|
Are you perhaps using McQuarrie and Simon's <i>Physical Chemistry: A Molecular Approach</i> as a rough outline? I ask because I have the
pchem texts of Atkins, McQuarrie, and Levine but only the McQuarrie has a math chapter on complex numbers following the first quantum theory
historical/background chapter. Or this could be simple coincidence.
The McQuarrie is my favorite of the 3 I have named above. It is the only one that builds up classical thermodynamics from quantum micro-foundations
instead of following a more historical order of discovery.
PGP Key and corresponding e-mail address
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by Polverone  | Are you perhaps using McQuarrie and Simon's <i>Physical Chemistry: A Molecular Approach</i> as a rough outline? I ask because I have the
pchem texts of Atkins, McQuarrie, and Levine but only the McQuarrie has a math chapter on complex numbers following the first quantum theory
historical/background chapter. Or this could be simple coincidence.
|
Unfortunately I can neither claim genius nor having read that textbook. It occurred to me to briefly introduce complex numbers under the assumption
that most here would have only scant knowledge of them.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Thanks AAHD!
|
|
|
neptunium
National Hazard
   
Posts: 985
Registered: 12-12-2011
Location: between Uranium and Plutonium
Member Is Offline
|
|
I remember a teacher long ago explaining to me complex numbers as a 3D volume, any point within it has an imaginary and a real coordinate . that
helped me understand better...
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by neptunium  | | I remember a teacher long ago explaining to me complex numbers as a 3D volume, any point within it has an imaginary and a real coordinate . that
helped me understand better... |
https://en.wikipedia.org/wiki/Complex_number
2D (the Complex Plane), yes. But 3D?
[Edited on 11-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
"Moreover, C has a nontrivial involutive automorphism x ↦ x* (namely the complex conjugation)"
*pop* there go some more brain cells.
i'll desperately cling onto this bit :-
"its complex conjugate ψ* , that is ψ*ψ is always a Real Number."
... and hope that when i hit an equation containing sqrt(-1) that it can be used to carry on to a real solution.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | "Moreover, C has a nontrivial involutive automorphism x ↦ x* (namely the complex conjugation)"
*pop* there go some more brain cells.
i'll desperately cling onto this bit :-
"its complex conjugate ψ* , that is ψ*ψ is always a Real Number."
... and hope that when i hit an equation containing sqrt(-1) that it can be used to carry on to a real solution. |
ψ<sup>*</sup>ψ in other, related parts of math and QM is also known as the Inner Product.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
The Wave function ψ (psi, “pseye”) - The Heart of the Beast (at least for WM):
This is probably the most abstract part of the course so far and much will become clearer once we get to the Schrodinger equation. Students should
nevertheless familiarise themselves with the following points. ‘Bookmark’ these prominently to make it easier to return to when necessary. For now
the wave function will remain slightly mysterious.
At the end of this module another interlude to allow non-calculus people to catch a glimpse into Derivatives/Differential Equations.
The Wave function ψ
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/wvfun.htm...
(Don't follow any links yet)
Wave function properties
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/wvfun.htm...
(Don't follow any links yet)
Constraints on the wave function
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/qm.html#c...
(Don't follow any links yet)
Another brief math interlude: derivatives of mathematical functions
QM/WM relies strongly on so called Differential Equations. In this course we’ll rarely (if at all) solve any of these but we’ll encounter some of
them. So without going into Calculus, let’s have a look at what is a Derivative (First and Second) by means of a concrete example.
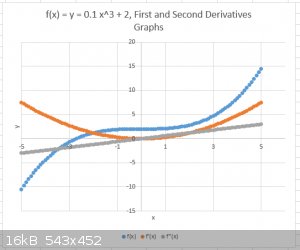
Take a simple function of x, like y = x<sup>3</sup>/10 + 2 = f(x) (“x raised to the power 3, divide that result by 10, then add 2”).
A few function values are x = 0; y = 2, x = 4; y = 2.8; x = -1, y = 1.9, obtained of course by plugging the x value into the function formula.
Below I’ve plotted y = x<sup>3</sup>/10 + 2 (blue) (as well as the First (amber) and Second Derivatives (grey)) for a range of x = - 5
to + 5). All three are smooth and continuous functions.
Note that the function f(x) is far from a straight line (the function is not linear), so that the slope (or gradient, syn.) of the curve changes as x
varies. The slope can be visualised by taking a point on the curve at x and drawing a straight line through this point, parallel to the curve itself
(a so called tangent). This can be repeated for each value of x.
Look at the slope a bit while imagining driving a car from x = - 5 to x = + 5. The first bit is the hardest: it's uphill and the slope is
greatest. Things really easy off at around x = 0 which is a brief plateau. Then things get progressively harder again as slope increases continually
from x = 0 to x = +5.
But Calculus can be used to generate a general expression for the slope, called the First Derivative and which can be denoted as δy/δx (or
δf(x)/δx)) or f’(x).
In the case of our example function:
y = x<sup>3</sup>/10 + 2
δy/δx = 3/10 x<sup>2</sup> = 0.3 x<sup>2</sup> = f’(x).
This new function, also denoted as f’(x) (“f prime of x”) or y’ can be plotted too, as shown on the graph in amber.
It needs to be understood that there is an f’(x) for each f(x). Math practitioners use tables with differentiating rules to tell them which is the
First Derivative f’(x) of a given function f(x).
The new function f’(x) can itself be differentiated, resulting in the Second Derivative of f(x), namely f’’(x) (“f second of x”) or y’’,
plot shown in grey.
In the case of the example f’’(x) = δ<sup>2</sup>y/δx<sup>2</sup> = 0.6 x
The Second Derivative is also noted as δ<sup>2</sup>y/δx<sup>2</sup> and this notation applied to the wave function ψ, as
δ<sup>2</sup>ψ/δx<sup>2</sup>, will be frequently encountered in QM/WM.
Summarising notation:
Function ============ > y or f(x)
First Derivative ======= > y’; f’(x) or δy/δx
Second Derivative ===== > y’’, f’’(x) or δ<sup>2</sup>y/δx<sup>2</sup>
Differential Equations
A Differential Equation is an equation in which First or Second (or Higher) Derivatives of a function occur.
[Edited on 11-7-2015 by blogfast25]
|
|
|
neptunium
National Hazard
   
Posts: 985
Registered: 12-12-2011
Location: between Uranium and Plutonium
Member Is Offline
|
|
go on Blogfast25! its been a while but its a good refresher! i like this..
lets get to the probabilty ..
|
|
|
Magpie
lab constructor
    
Posts: 5939
Registered: 1-11-2003
Location: USA
Member Is Offline
Mood: Chemistry: the subtle science.
|
|
Quote: Originally posted by blogfast25  | The Wave function ψ (psi, “pseye”) - The Heart of the Beast (at least for WM):
This is probably the most abstract part of the course so far and much will become clearer once we get to the Schrodinger equation.
|
What's clear about pitchforks?
The single most important condition for a successful synthesis is good mixing - Nicodem
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Pitchforks are the only way to get a reluctant student to study properly IMHO.
Zombie's smoking behind the bicycle shed again, so we may as well get on ...
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
You feel ready for it? Pitchforks coming up in spades, in that case!
[Edited on 12-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Onwards and Sideways !
... as my one-legged Grandafther always said.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Time independent Schrodinger equation
I’ll be limiting our course to the time independent Schrodinger, which concerns itself with mainly Quantum Systems of constant energy. Also, for
starters we’ll limit it to one dimension only.
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/scheq.htm...
Okay, so that’s not something you want to write on your Facebook wall. But what does it mean??
Let’s start with the right hand side of the equation:
Eψ(x)
This is the product of the particle’s Total Energy E and the wave function ψ(x).
Note that the total energy is written as E and not E(x). E is not a function of x but a Real Number that can take on discrete values,
known as Eigenvalues of the Schrodinger equation. Together with the right wave function ψ(x), the right value of E provide a mathematical solution of
the Schrodinger equation.
Now look at the second term of the left hand side of the equation:
U(x)ψ(x)
This is the product of the Potential Energy U(x) and the wave function ψ(x). Note that here U(x) really is a function of x: over the range of x
values where the particle ‘roams’ it cannot be assumed a priori that U remains invariant of x. Later we’ll see some ‘real life’
Potential Energy functions that can apply to particles, including to an electron bound to a nucleus, in other words a hydrogen atom.
Well, dear QMSMers, we’ve got a total energy related term on the right and one potential energy term on the left, rara, what could the left hand
term be related to? Kinetic Energy perhaps?
Correct! The term:
- (ћ<sup>2</sup>/2m) δ<sup>2</sup>ψ(x)/δx<sup>2</sup>
(With ћ = h/(2π) (“h bar”))
… is related to the Kinetic Energy of the particle wave.
The Schrodinger equation is thus a kind of Energy Conservation Equation (E = U + E<sub>kin</sub> of Quantum Physics. of Quantum Physics.
In three dimensions:
The time independent can easily be expanded into three dimensional domains (or two dimensional ones, for that matter).
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/sch3d.htm...
[Edited on 12-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Woah ! This horse is going crazy !
This will take a bit of Time to digest, and even grab the ends of.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Time will be granted. Try not to get lost in side issues (links) just yet.
Good night and good luck. 
[Edited on 12-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
OK. Digested as much as i can, yet have to admit that i am a bit lost, already.
".. a kind of Energy Conservation Equation (E = U + Ekin)"
That makes a sort of sense, but where does it lead to ?
Some kind of roadmap of where we're going would be of great help.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
We're going many places but one very important one on the roadmap is to find out which states of total energy E are allowed for a given quantum system
(atom, molecule or other). An equation (or equivalent of) like E = U + E<sub>kin</sub> is useful for that. It was Schrodinger's intention
when he set up his famous equation.
The Schrodinger equation yields solutions for ψ, associated with allowable values of E.
ψ, in the case of an atom or a molecule gives us information on the whereabouts of the electron(s).
In the coming episode I'll use a specific quantum system to illustrate this.
Tell me when you're ready.
[Edited on 15-7-2015 by blogfast25]
|
|
|
Metacelsus
International Hazard
    
Posts: 2531
Registered: 26-12-2012
Location: Boston, MA
Member Is Offline
Mood: Double, double, toil and trouble
|
|
I have taken courses in linear algebra and vector calculus (but not Q.M.) so I know basically what the equation means mathematically. My question is:
what does the constant factor (-Hbar^2/2m) physically mean?
[Edited on 15-7-2015 by Cheddite Cheese]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
It doesn't really matter, for my purposes here. You could rewrite the SE as:
aΨ" + UΨ = EΨ (Ψ" is the second derivative of Ψ)
... with a the proportionality constant you're asking about. Its precise form - ћ<sup>2</sup>/2m was arrived at when
Schrodinger set up the equation heuristically. You can find the derivation of the SE in Wiki, if you want to delve deeper. I won't be doing that here.
Again, it should become clearer as we go on.
Historical development of the SE:
https://en.wikipedia.org/wiki/Schr%C3%B6dinger_equation#Hist...
[Edited on 15-7-2015 by blogfast25]
|
|
|
| Pages:
1
2
3
4
..
33 |