blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Solvation of ionic compounds in water: basic theory and examples
::Topics::
1. Gibbs Free Energy of dissolution
1.1. Entropy of dissolution
1.2. Enthalpy of dissolution
2. Solubility limits and Solubility products
2.1. Hydrolysis and pH effects
2.2. Common ion effect
2.3. Ionic strength effect
2.4. Cation/anion size effects
Coming soon. Suggestions welcome! 
[Edited on 11-2-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
1. Gibbs Free Energy of dissolution.
Dissolution of a substance (the solute) into a solvent is a process involving a change of state:
$$\text{solute}+\text{solvent} \to \text{solution}$$
In this change of state, consider the left hand side as State 1 and the right hand side as State 2.
Thermodynamics dictates that for this change of state to be thermodynamically favourable the change in Gibbs Free Energy has to be negative:
$$\Delta G = G_2-G_1<0$$
And with:
$$\Delta G =\Delta H-T\Delta S$$
And:
$$\Delta H=H_2-H_1, \Delta S=S_2-S_1$$
H, S and T are Enthalpy, Entropy and absolute temperature respectively.
Note that a negative predicted ΔG does not imply spontaneity or speed. Add some sugar to your tea and don’t stir. The sugar will basically not
dissolve at all (or rather, it would take almost eternity to fully dissolve), until we give the tea a quick stir and the sugar then dissolves very
swiftly.
1.1. Entropy of dissolution:
On the concept of Entropy entire libraries have been dedicated and I’m not about to add more to it. Instead let’s apply a more narrow
understanding of it to the process of dissolution.
In the schematic below, 8 molecules of solute (black balls) and 8 molecules of solvent (white squares) are in a container, in various degrees of
mixing.
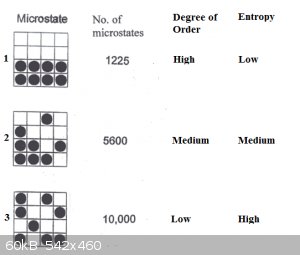
State 1: complete separation between solute and solvent (think sugar at the bottom of that teacup, unstirred). It would be a mistake to think
that only one such arrangement exists. Not at all: if we label the molecules we can create many swaps that amount to the same arrangement. There are
in fact 1225 permutations of the same arrangement.
State 2: a mere 2 out of 8 solute molecules have strayed from their initial positions. The number of permutations possible is now already
dramatically higher: about 5600.
State 3: only 3 out of 8 solute molecules are in their original positions: the number of permutations possible is now about 10000.
It’s obvious from this that there are far more disordered arrangements than ordered ones and that disordered ones have far higher numbers of
possible permutations.
In short, disordered systems are far more probable than ordered ones. We say they have higher Entropy.
Two important conclusions can be drawn here:
a. Dissolution always increases entropy of the system:
$$\Delta S >0$$
And since as:
$$\Delta G=\Delta H-T\Delta S<0$$
... the Entropy increase always favours dissolution, as T is always positive.
b. Dissolution is essentially irreversible: in a solution left unchanged the solute will not at some time magically rearrange at the
bottom of the container because that is simply too improbable to happen.
[Edited on 12-2-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
1.2. Enthalpy of dissolution:
For dissolution of ionic compounds to happen several Enthalpies come into play.
a. Lattice energy:
A solid ionic compound is held together by the Coulombic attractions between cations and anions. To change state from ionic lattice + solvent
to solution these Coulombic attractions (SM thread) have to be overcome and that costs energy. Bar any other Enthalpic effects, dissolution would always be
endothermic (and frequently it is).
b. Coulombic attraction between dissolved ions and water dipoles:
Due to their molecular structure water molecules are permanent electric dipoles (SM thread), with the O atoms carrying a partial negative charge and the H atoms a partial positive charge. Ions are
charged atoms and emit an electric field. Water dipoles orient themselves into that field, as in the schematic for a sodium cation and its water cloud
below:
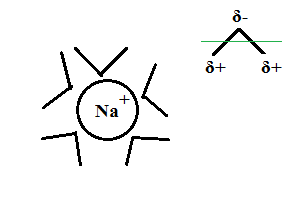
This orientation lowers potential energy of the system somewhat and converts it to Enthalpy.
c. Complexation with solvent:
Many cations form stable coordination complexes with water (SM thread). These processes are exo-energetic (ΔG < 0).
<hr>
So... is a compound soluble or insoluble?
$$\Delta G =\Delta H-T\Delta S<0$$
We’ve already established that the term – TΔS is always negative, so for the above condition to be satisfied we have:
$$\Delta H < T \Delta S$$
Where ΔH is the sum of the Enthalpies discussed above.
Simple example: KCl
For KCl (dissolution) ΔH = + 8.4 kJ/mol and ΔS = 96 J/mol K. At 25 C we get:
ΔG = 8.4 kJ/mol – 298 K x 96 J/mol K = - 20 kJ/mol.
So KCl is water soluble and without addition of heat, dissolving KCl in water cools down that solution (a little).
[Edited on 12-2-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
2. Solubility limits and Solubility products:
Solubility limits of soluble ionic compounds are of course easy to find, even in a broad range of temperatures (see e.g. Wikipedia’s solubility
table). Far more interesting in my opinion are those ionic compounds that are poorly soluble or even categorised as ‘insoluble’.
Dissolution then becomes a left leaning equilibrium between two states:
$$\text{solute}+\text{solvent} \leftrightarrow \text{solution}$$
For a generic ionic compound we can specify:
$$\mathrm{M_nA_m}(s) \leftrightarrow n\mathrm{M^{m+}}(aq) +m\mathrm{A^{n-}}(aq)$$
As with all equilibria, an equilibrium constant, here known as the solubility product, can be defined:
$$K_{sp}=[\mathrm{M^{m+}}]^n[\mathrm{A^{n-}}]^m$$
... where the bracketed quantities are concentrations.
Thermodynamically, insoluble compounds correspond to:
$$\Delta G_{solvation}>0$$
Which via Nernst means:
$$K_{sp} \ll 1$$
Relation between K<sub>sp</sub> and solubility limit:
Let’s assume our generic ionic compound has a solubility limit of S mol/L.
Each mol of the compound dissociates into n mol of cations and m mol of anions, so:
$$K_{sp}=(nS)^n(mS)^m$$
$$K_{sp}=n^nm^m(S)^{n+m}$$
$$S=\sqrt[n+m]{\frac{K_{sp}}{n^nm^m}}$$
Example: BaF<sub>2</sub>
K<sub>sp</sub> = 1.0 x 10<sup>-6</sup>
$$1.0 \times 10^{-6}=S \times (2S)^2$$
$$1.0 \times 10^{-6}=4S^3$$
$$S=0.006\:\mathrm{mol/L}$$
(Note that hydrolysis of the F<sup>-</sup> has been ignored here, see next post)
<hr>
Some more basic free energy considerations:
Below we’ll use the simple example of a binary, ionic compound MX. The suffixes “sp”, “L” and “aq” refer to dissolution, lattice and
aquation, respectively.
Nernst, applied to the process of dissolution, tells us:
$$\Delta G_{sp}=-RT\ln K_{sp}=\Delta H-T\Delta S$$
Reworked:
$$\ln K_{sp}=-\frac{\Delta H}{RT}+\frac{\Delta S}{T}$$
Simple examination of the last equation shows that a ten-fold change in Ksp will result in a change of less than 6 kJ/mol in the free
energy of solution. This means that energetic differences between soluble and insoluble salts are small. Laboratory experience confirms that
dissolution processes are by and large not highly energetic.
To analyze the changes it is useful to think in terms of the following cycle:
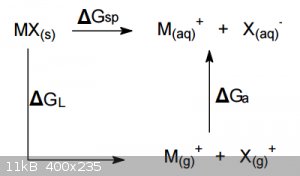
where ∆G<sub>sp</sub> is the free energy of dissolution and must be equal to ∆G<sub>L</sub>, the free energy of
vapourisation of MX to non-interacting gaseous cations and anions plus ∆G<sub>a</sub>, the free energy of aquation (or solvation if the
solvent is something other than water). The latter term is obviously the sum of the separate free energies of aquation of the cation and the anion.
∆G<sub>sp</sub> is generally rather small, between -80 and +80 kJ/mol, while both ∆G<sub>L</sub> and ∆G<sub>a
</sub> are both very large and of opposite sign. Remember that ∆G<sub>L</sub> is essentially the lattice energy (but not entirely,
since the work of expansion and the entropies of the ions themselves must be included), which is always >400 kJ/mol and may be as high as >3000
kJ/mol.
Thus the solubility of a salt is in effect determined by a small difference between two large numbers.
[Edited on 14-2-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
2.1. Hydrolysis and pH effects - worked examples:
a. BaF<sub>2</sub> example:
In the example of the previous post we neglected that fluoride is the conjugated base of a weak acid and thus itself a weak base:
$$\mathrm{F}^- (aq) + \mathrm{H_2O}(l) \leftrightarrow \mathrm{HF}(aq)+\mathrm{OH}^{-}$$
Ignoring the auto-dissociation of water and with the following equations:
$$K_a=\frac{[\mathrm{H_3O^+}][\mathrm{F^-}]}{[\mathrm{HF}]}$$
$$K_{sp}=[\mathrm{Ba^{2+}}][\mathrm{F^-}]^2$$
$$[\mathrm{Ba^{2+}}]=\frac12[\mathrm{F^-}]+\frac12[\mathrm{HF}]$$
$$S=[\mathrm{Ba^{2+}}]$$
With some reworking we get:
$$S=\sqrt[3]{\frac{K_{sp}}{4}\Big(1+\frac{[\mathrm{H_3O^+}]}{K_a}\Big)^2}$$
Closer inspection shows that this is the result obtained when ignoring hydrolysis, multiplied by this pH dependent factor:
$$\sqrt[3]{\Big(1+\frac{[\mathrm{H_3O^+}]}{K_a}\Big)^2}$$
As this is a continuously increasing function of [H<sub>3</sub>O<sup>+</sup>], solubility increases with decreasing pH.
b. Calcium carbonate:
Ignoring hydrolysis of the carbonate ions the solubility would simply be:
$$S=\sqrt{K_{sp}}$$
Taking hydrolysis into account, that result has to be multiplied by the following pH dependent correction factor:
$$\sqrt{1+\frac{[\mathrm{H_3O^+}]}{K_{a,2}}}$$
The strong influence of pH on CaCO<sub>3</sub> solubility can be seen from the correction factor:
46 at pH = 7
460 at pH = 5
4600 at pH = 3
c. D-block sulphides (mainly):
Sulphides are the salts of a very weak diprotic acid and their solubility therefore depends on pH.
A few sulphide solubility products:
CdS: 8 x 10<sup>-28</sup>
CuS: 6 x 10<sup>-37</sup>
MnS: 3 x 10<sup>-14</sup>
PbS: 3 x10<sup>-28</sup>
NiS: 3 x 10<sup>-19</sup>
Ag2S: 6 x 10<sup>-51</sup>
ZnS: 2 x 10<sup>-25</sup>
Source.
The two deprotonation constants are of H<sub>2</sub>S are:
$$K_{a,1}=\frac{[\mathrm{H_3O^+}][\mathrm{HS^-}]}{[\mathrm{H_2S}]}=10^{-7}$$
$$K_{a,2}=\frac{[\mathrm{H_3O^+}][\mathrm{S^{2-}}]}{[\mathrm{HS^-}]}=10^{-19}$$
This graph shows the relative concentrations of H<sub>2</sub>S, HS<sup>-</sup> and S<sup>2-</sup> in function of
pH:
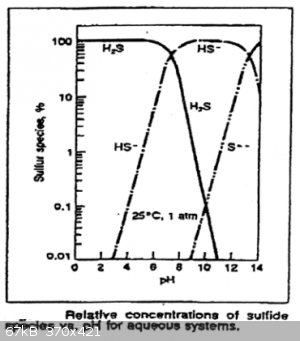
Multiplying the first two equations with each other we get:
$$K_{a,1}K_{a,2}=\frac{[\mathrm{H_3O^+}]^2[\mathrm{S^{2-}}]}{[\mathrm{H_2S}]}=10^{-26}$$
$$[\mathrm{S^{2-}}]=10^{-26}\frac{[\mathrm{H_2S}]}{[\mathrm{H_3O^+}]^2}$$
Literature puts the solubility of H<sub>2</sub>S at about 0.1 M and quite invariant of pH, so we can write:
$$[\mathrm{S^{2-}}]\approx \frac{10^{-27}}{[\mathrm{H_3O^+}]^2}$$
For a generic sulphide MS:
$$K_{sp}=[\mathrm{M^{2+}}][\mathrm{S^{2-}}]$$
Combining and for [M<sup>2+</sup>] = 0.1 mol/L:
$$[\mathrm{H_3O^+}] \approx \frac{10^{-14}}{\sqrt{K_{sp}}}$$
We can also rewrite it using p-functions (- log) as:
$$pH \approx 14 -\frac12 pK_{sp}$$
Now what does this calculated pH really represent? If we take a solution of approx. 0.1 M [M<sup>2+</sup>] and saturate
it with H<sub>2</sub>S gas, control the pH (by buffering, e.g.), then the above calculated pH is the maximum value for which no MS
precipitate forms. Above that pH the sulphide concentration is too high for M<sup>2+</sup> to stay in solution.
For a few of the less insoluble sulphides listed above:
MnS: pH > 7 to obtain precipitation.
NiS: pH > 5 to obtain precipitation.
ZnS: pH > 1.7 to obtain precipitation.
It also follows that sulphides with a pK<sub>sp</sub> > 26 will always precipitate, regardless of pH.
d. pH Selective precipitation of hydroxides - Fe(+3)/Mn(+2) separation:
A dilute (< 1 M) solution of manganous and ferric salts is first part neutralised with ammonia solution until only the small amount of permanent
precipitate forms. About ¾ is then set aside (Part A) and the rest treated with ammonia solution to precipitate the metals as hydroxides (Part B).
Part B is filtered and the filter cake washed free of ammonia and ammonia salts. The washed filter cake is then added to Part A and allowed to stand
overnight, occasionally stirring.
After filtration, a solution is obtained that is free of ferric ions, because at the pH of Part A + filter cake B, ferric ions only exists as
insoluble ferric hydroxide. Mn(+2) stays in solution. This is due to the immense difference of the solubility products of both hydroxides:
Fe(OH)<sub>3</sub>: 4 x 10<sup>-38</sup>
Mn(OH)<sub>2</sub>: 1.9 x 10<sup>-13</sup>
This separation method has been discussed and successfully used by several SM members, myself included. There’s also a ‘Nurdrage’ YouTube demo
on it.
[Edited on 15-2-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
2.2. Common ion effect:
If for a simple ionic compound MA we write the dissolution equilibrium:
$$\mathrm{MA}(s) \leftrightarrow \mathrm{M^+}(aq) + \mathrm{A^-}(aq)$$
... then if we increase the concentration of either the cations or the anions the equilibrium will shift to the left in accordance with the Le
Chatelier Principle. As a result, solubility is suppressed.
Let’s look at it analytically with calcium hydroxide as example: K<sub>sp</sub> = 5.5 x 10<sup>-6</sup>.
We can estimate the solubility S in pure water the usual way:
$$K_{sp}=S(2S)^2$$
So, S = 0.011 M.
Now let’s assume we start from a 0.1 M NaOH solution, add Ca(OH)<sub>2</sub> to it and stir until equilibrium is achieved and the
Ca(OH)<sub>2</sub> concentration has reached x mol/L, then:
$$S=[\mathrm{Ca^{2+}}]=x, [\mathrm{OH^-}]=0.1+2x$$
And using the solubility product:
$$K_{sp}=x(0.1+2x)^2$$
Which reworked yields:
$$4x^3+0.4x^2+0.01x-5.5 \times 10^{-6}=0$$
A third degree polynomial and with Wolfram Alpha to the rescue we get:
x = S = 0.00054 M, or about 200 x less than in the case of pure water.
But notice also this:
$$x \ll 0.1$$
So:
$$0.1+2x \approx 0.1$$
$$K_{sp} \approx x(0.1)^2$$
Then x = S = 0.00055 M, very close to the polynomial solution.
Broadly we can say if C is the concentration of the added common ion and complies to:
$$C\gg K_{sp}$$
Then the above approximation will hold.
Let’s apply this to the case where we dissolve Ca(OH)<sub>2</sub> in 0.1 M CaCl<sub>2</sub>:
$$K_{sp}=(0.1 +x)(2x)^2$$
And with a similar approximation as above:
$$K_{sp} \approx 0.4x^2$$
x = S = 0.0037 M
(The exact solution is 0.0036 M)
Note that the solubility suppression effect is stronger for NaOH than for CaCl<sub>2</sub>: that is of course the power of... the power of
2!
Where the common ion effect does not apply:
Just a few examples:
• Hydroxide solution and amphoteric metal hydroxides will in fact increase the solubility of the latter.
• Various complexations like AgCl to AgCl2<sup>-</sup>, AgCN to Ag(CN)2<sup>-</sup>, PbCl2
to PbCl4<sup>2-</sup> and others cause addition of the anion to the solution to increase solute solubility.
[Edited on 17-2-2016 by blogfast25]
|
|
|
MrHomeScientist
International Hazard
    
Posts: 1806
Registered: 24-10-2010
Location: Flerovium
Member Is Offline
Mood: No Mood
|
|
Really great resource here. Thanks for volunteering to share your knowledge!
One question on this segment:
| Quote: | The strong influence of pH on CaCO<sub>3</sub> solubility can be seen from the correction factor:
46 at pH = 7
460 at pH = 5
4600 at pH = 3 |
"Solubility" there is a bit misleading, isn't it? Because at low pH CaCO<sub>3</sub> ceases to be the carbonate, as
CO<sub>2</sub> escapes. Making it really only "half soluble" so to speak.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Thanks!
Quote: Originally posted by MrHomeScientist  | Really great resource here. Thanks for volunteering to share your knowledge!
One question on this segment:
| Quote: | The strong influence of pH on CaCO<sub>3</sub> solubility can be seen from the correction factor:
46 at pH = 7
460 at pH = 5
4600 at pH = 3 |
"Solubility" there is a bit misleading, isn't it? Because at low pH CaCO<sub>3</sub> ceases to be the carbonate, as
CO<sub>2</sub> escapes. Making it really only "half soluble" so to speak. |
At even lower pH a carbonate dissolves completely to a calcium salt, yet do we not claim "calcium carbonate dissolves in acid"? Same with many
metals. It becomes semantics, to me. 
Incidentally, even at pH = 7, CaCO3 solutions contain significant amounts of HCO3<sup>-</sup>, which is precisely
what brings about the greater solubility, compared to what to expect from:
$$S=\sqrt{K_{sp}}$$
[Edited on 17-2-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
2.3. Ionic strength effect:
Due the formation (simply put) of so-called ionic atmospheres around cations and anions their interaction is reduced due to shielding.
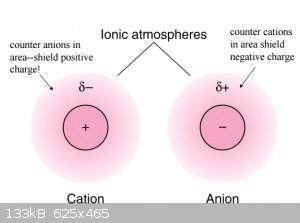
To quantify this, the concept of chemical activity (which is not limited to solvated species) is introduced:
$$a_C=\gamma [C]$$
From Debeye-Huckel’s theory of electrolytes we have an approximate and workable description of the activity coefficient γ:
$$\log \gamma \approx -Az^2\frac{\sqrt{I}}{1+\sqrt{I}}$$
Where:
$$A=0.509\:\mathrm{mol^{-0.5}kg^{0.5}}$$
Where I is the ionic strength of the solution:
$$I=\frac12\sum_{i=1}^n C_iz_i^2$$
E.g. for a solution 0.3 KNO3 + 0.1 MgSO4, then I = 0.7. Note that for pure water I = 0.
The following tool is useful to estimate ionic strengths and activity coefficients (for mono and divalent ions):
http://www.lenntech.com/calculators/activity/activity-coeffi...
Make sure you select the correct units.
The function:
$$\gamma=10^{-\log \gamma}$$
... is worth exploring briefly. Look at the argument:
$$I \to 0, \frac{\sqrt{I}}{1+\sqrt{I}} \to 0$$
So :
$$I \to 0, \gamma \to 1$$
For infinitely diluted solutions, the activity coefficient tends to unity.
Also:
$$I \to \infty, \frac{\sqrt{I}}{1+\sqrt{I}} \to 1$$
$$I \to \infty, \gamma \to 10^{-Az^2}$$
For a simple, poorly soluble compound MA:
$$K_{sp}=\gamma_M[M^{z+}]\gamma_A[A^{z-}]$$
$$K_{sp}=\gamma^2S^2$$
$$S=\frac{\sqrt{K_{sp}}}{\gamma}$$
a. Case of CaSO4 in pure water:
Ksp = 4.93 x 10<sup>-5</sup>, S = 2.1 g/L (Wikipedia)
$$\log \gamma= -Az^2\frac{\sqrt{I}}{1+\sqrt{I}}$$
$$\gamma=10^{-\log \gamma}$$
$$I=\frac12([Ca^{2+}] \times 2^2+[SO_4^{2-}]\times ^2)=4S$$
$$S=\frac{\sqrt{K_{sp}}}{\gamma}$$
The problem is that this is a transcendental equation that has no analytical solution. Instead we need to use a numerical, iterative approach.
Creating an Excel spread for this task is easy but not even necessary.
As a starting point, assume γ = 1 and calculate the first approximation of S:
$$S_1=\frac{\sqrt{K_{sp}}}{\gamma}=0.00702\:\mathrm{M}$$
Now insert this value into the tool mentioned above, for calcium and sulphate and obtain a new value for γ. Use this new value to obtain the next
approximation of S. Adjust the calcium and sulphate to obtain a new value of γ.
I repeated this process 8 times and S then converged to 0.019 M, more than twice the original value. 0.019 M corresponds to about 2.6 g/L, so not too
far from Wiki’s stated 2.1 g/L.
b. With 0.1 KNO3:
The same method can be used to estimate calcium sulphate in (e.g.) 0.1 M potassium nitrate.
We can even use a little shortcut because we already know the solubility in pure water: 0.019 M. Use that value with the tool, adding also 0.1 M
potassium and 0.1 M nitrate, this gives a starting point γ = 0.256. Use this to calculate the next approximation of S, adjust the tool for the next
γ, etc.
Only 5 iterations were needed to converge on S = 0.0308 M, an increase of about 50 % with respect to pure water.
c. With common ion effect: 0.1 M Na2SO4:
$$K_{sp}=\gamma^2S(S+0.1)$$
$$\gamma^2S^2+0.1\gamma^2 S-K_{sp}=0$$
First, using the tool, estimate γ for S = 0, sodium = 0.2 M and sulphate = 0.1 M.
Using that value for γ, obtain the first estimate of S by finding the positive root of the quadratic equation (I used Wolfram Alpha because the
equation’s coefficients can then be adjusted easily for subsequent iterations). Adjust the ionic strength for calcium and sulphate using the tool
and obtain the next estimate of γ.
Recalculate S and continue to iterate until S converges. It took about 4 iterations to settle on S = 0.00208 M. Note that this is about 10 x less than
the calculated value for pure water.
[Edited on 18-2-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
2.4. Cation/anion size effects:
As we saw in this previous post, of the two terms ΔhydrH and TΔhydrS , the dominant factor in determining the magnitude of
ΔhydrG is ΔhydrH . Similarly, for ΔlatticeG, the dominant factor is ΔlatticeH. So, in considering the
relationship between the solubility of a salt and the sizes of the component ions, we turn our attention to the relationships between rion,
ΔhydrH and ΔlatticeH given in equations below. The actual values of ΔhydrH and ΔlatticeH are always
negative.
$$\Delta_{lattice}H \propto \frac{1}{r_++r_-}$$
$$\Delta_{hydr}H \propto \frac{1}{r_+}+\frac{1}{r_-}$$
Now consider the application of these two expressions to a series of salts of similar lattice type. For a series of MX salts where X is constant and M
varies, if r+ < r-, the first shows that there will be little variation in ΔlatticeH.
However, upon dissolution, if r+ < r-, ΔhydrH (cation) will be much more negative than ΔhydrH (anion) for all values of r-.
Thus, ΔhydrH will be roughly proportional to 1/ r+ . Thus, along a series of related salts with increasing r+, but with r+ < r-,
ΔlatticeH will remain nearly constant while ΔhydrH becomes less negative. Hence, ΔsolH (and thus ΔsolG ) will
become less negative and solubility will decrease. Such a series is exemplified by the alkali metal hexachloroplatinates and alkali metal
hexachlorostannates.
Even more generally we can say the greater difference in size between cations and anions increases solubility as exemplified also by sodium halides
and silver(I) halides.
|
|
|
|