| Pages:
1
..
31
32
33 |
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
OK. I get the message.
Sorry for changing B&D Uni a bit.
Selling the walls, doors and roof tiles was just for Profit, which is just Business, so no hard feelings.
As it happens i'm in a position to put back at least half the roof tiles, 4 of the doors (one has no handles) even a wall or three.
I'll even chuck yer in a cupl'a dags. C'mon !
Mi mate John says he has a Big job goin', and might need to stash a tiny little particle accellerator in the basement, maybe a bit of the county too,
for a year or so ...
Deal ?
(don't be fergetting de bonus dags now - dey needs a feed now and ag'in)
|
|
|
Dan Vizine
National Hazard
   
Posts: 628
Registered: 4-4-2014
Location: Tonawanda, New York
Member Is Online
Mood: High Resistance
|
|
So, has blogfast25 left the building?
2 1/2 months without a word. That would normally have been over 200 posts.
I know an illness was mentioned by him, and there was a bit of drama.
His presence is surely missed.
"All Your Children Are Poor Unfortunate Victims of Lies You Believe, a Plague Upon Your Ignorance that Keeps the Youth from the Truth They
Deserve"...F. Zappa
|
|
|
j_sum1
Administrator
       
Posts: 6229
Registered: 4-10-2014
Location: Unmoved
Member Is Offline
Mood: Organised
|
|
Agreed. This has been raised before.
I don't know that anyone knows for sure.
Maybe aga knows???
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Nope. No idea.
Tried U2U, all known emails, and a phone call, with no luck.
I hope that 'chemistry bust' thing didn't turn out horribly.
Definitely missing bloggers' presence.
|
|
|
Corrosive Joeseph
National Hazard
   
Posts: 915
Registered: 17-5-2015
Location: The Other Place
Member Is Offline
Mood: Cyclic
|
|
Yup................. His absence is a major loss to the forum and he is sorely missed..................
Here's wishing him the best of luck wherever he is and hoping to see him post here again.............
Gentlemen, raise yer flasks and toast, 'To Blogfast', wherever he is...................
/CJ
Being well adjusted to a sick society is no measure of one's mental health
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Wave functions: 1D Hydrogen atom
A few years ago I posted at SM on this subject. What follows is a cleaned-up, modernised version of that post. It is an interesting exercise in
heuristic derivation of wave functions of a simple quantum system.
The 1D hydrogen atom:
A proton and an electron are held in an infinite 1D box:
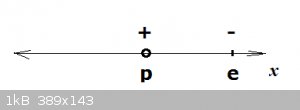
x represents simply the distance between the proton and the electron. The former is considered immobile (due to the high mass
ratios).
The Schrödinger equation for the 1D hydrogen atom:
Since as we're looking for stationary, bound states, we can use the time independent SE (TISE), here in all its glory and elegance:
$$\hat{H}u=Eu$$
Applying the Hamiltonian (total energy) operator to the wave function should yield the wave function, multiplied with the (total) energy
eigenvalues E.
I'm using "u" instead of "psi" for the wave function, for ease of notation.
The Hamiltonian operator of the system is:
$$\hat{H}=-\frac{\hbar^2}{2m}\nabla^2+U(x)$$
Where:
$$\nabla^2=\frac{\mathrm{d^2}}{\mathrm{dx^2}}$$
And:
$$U(x)=-\frac{\alpha}{x}$$
Where:
$$\alpha=\frac{e^2}{4\pi \epsilon_0}$$
So we get:
$$u''+\frac{2m\alpha}{\hbar^2}\frac{1}{x}u=-\frac{2mE}{\hbar^2}u$$
Because:
$$E<0\implies -\frac{2mE}{\hbar^2}>0$$
We call:
$$k^2=-\frac{2mE}{\hbar^2}>0$$
k is of course the wave number (see e.g. de Broglie). With some more substititions:
$$\beta=\frac{2m\alpha}{\hbar^2}=\frac{me^2}{2\pi \epsilon_0\hbar^2}$$
So the TISE becomes:
$$u''+\beta\frac{1}{x}u=k^2u$$
There are various ways of solving this non-homogeneous DE. I'll asume (Ansatz) that:
$$u=f(x)e^{-kx}$$
Where f(x) is some function of x, to be yet determined.
Continued below.
[Edited on 18-2-2017 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Some derivatives:
Using the Ansatz:
$$u=f(x)e^{-kx}$$
We can calculate a few derivatives:
$$u'=f'(x)e^{-kx}-kf(x)e^{-kx}=f'(x)e^{-kx}-ku$$
$$u''=f''(x)e^{-kx}-kf'(x)e^{-kx}-ku'$$
$$=f''(x)e^{-kx}-kf'(x)e^{-kx}-k[f'(x)e^{-kx}-kf(x)e^{-kx}]$$
$$=f''(x)e^{-kx}-2kf'(x)e^{-kx}+k^2f(x)e^{-kx}$$
Inserting these derivatives into the TISE (post above) and a little simplifying then yields:
$$\boxed{f''(x)-2kf'(x)+\beta\frac{1}{x}f(x)=0}$$
This new DE is the one f(x) needs to comply to, to provide a solution to the TISE.
Second Ansatz:
Now we make another educated guess (second Ansatz) re. the nature of f(x). I'll assume it to be of the polynomial form:
$$f(x)=x+a_1x^2+...+a_{i-1}x^i+...+a_{n-1}x^n$$
We can also write this as:
$$f(x)=x+\displaystyle \sum_{i=2}^n a_{i-1}x^i$$
Calculate the derivatives:
$$f'(x)=1+\displaystyle \sum_{i=2}^{n-1} ia_{i-1}x^{i-1}$$
$$f''(x)=\displaystyle \sum_{i=2}^{n-2} i(i-1)a_{i-1}x^{i-2}$$
And inserting into:
$$f''(x)-2kf'(x)+\beta\frac{1}{x}f(x)=0$$
... yields:
$$\displaystyle \sum_{i=2}^{n-2} i(i-1)a_{i-1}x^{i-2}-2k\Big[1+\displaystyle \sum_{i=2}^{n-1} ia_{i-1}x^{i-1}\Big]+\frac{\beta}{x}\Big[x+\displaystyle
\sum_{i=2}^n a_{i-1}x^i\Big]=0$$
Slightly reworked:
$$\displaystyle \sum_{i=2}^{n-2} i(i-1)a_{i-1}x^{i-2}-2k\Big[1+\displaystyle \sum_{i=2}^{n-1} ia_{i-1}x^{i-1}\Big]+\beta\Big[1+\displaystyle
\sum_{i=2}^n a_{i-1}x^{i-1}\Big]=0$$
This last expression is slightly clearer when written more explicitly:
$$(n-2)(n-3)a_{n-3}x^{n-2}+(n-1)(n-2)a_{n-2}x^{n-1}+...+i(i-1)a_{i-1}x^{i-2}+...+6a_2x^2+2a_1x$$
$$-2k[(n-1)a_{n-2}x^{n-2}+na_{n-1}x^{n-1}+...+ ia_{i-1}x^{i-1}+...+3a_2x^2+2a_1x+n]$$
$$+\beta[1+a_{n-1}x^{n-1}+...+a_{i-1}x^{i-1}+...+a_2x^2+a_1x]=0$$
This (very!) lengthy polynomial expression is true if the sums of terms of the same power of x are all zero.
Energy quantisation:
The stationary, bound states are expected to have discrete, quantised energy levels.
Using the terms for:
$$x^0$$
... we get:
$$-2kn+\beta=0$$
$$2kn=\beta \implies 4k^2n^2=\beta^2$$
$$ -4\frac{2mE}{\hbar^2}n^2=\beta^2$$
With back substitutions from above:
$$\boxed{E_n=-\frac{me^4}{128\pi^2\epsilon_0^2\hbar^2n^2}}\text{for: }n=1,2,3,...$$
Note that as for the 3D H-atom the quantisation is governed by:
$$E_n \propto \frac{1}{n^2}$$
As expected, ground state energy is non-zero and given by:
$$E_1=-\frac{me^4}{128\pi^2\epsilon_0^2\hbar^2}$$
Continued below: polynomial coefficients.
[Edited on 18-2-2017 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Polynomial coefficients:
Full determination of the wave functions requires determination of the polynomial coefficients:
$$a_1, a_2...a_i...a_n$$
This is easier than it may seem. From the lengthy polynomial above we can find for instance:
$$i(i-1)a_{i-1}x^{i-2}-2k(i-1)a_{i-2}x^{i-2}+\beta a_{i-2}x^{i-2}=0$$
Reworked with:
$$2kn=\beta$$
gives:
$$a_{i-1}=2k\frac{i-n-1}{i(i-1)}a_{i-2}$$
And reworked some more:
$$a_i=2k\frac{i-n}{i(i+1)}a_{i-1}$$
These recursive formulas allow to calculate all coefficients for any n and i.
Note that:
$$a_0=1$$
Let's calculate a few coefficients, for different n and i:
$$n=1, a_1=0$$
$$n=2, a_1=-k, a_2=0$$
$$n=3, a_1=-3k, a_2=k^2, a_3=0$$
$$n=4, a_1=-3k, a_2=2k^2, a_3=-\frac12 k^3$$
The wave function for (e.g.) n=4 is thus:
$$u_4(x)=(x-3kx^2+2k^2x^3-\frac12 k^3x^4)e^{-kx}$$
Note that these wave functions have not been normalised yet.
Continued below: normalisation, visualisation of wave functions and electron probability densities.
[Edited on 17-2-2017 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Normalisation, visualisation of wave functions and electron probability densities.
The wave functions above haven't been normalised yet. The general normalisation requirement (Born) can be written as:
$$\int_{\mathrm{domain}}|\psi|^2dV=1$$
For the ground state of the 1D H atom, we can write the normalised wave function as (a0=1, a1=0):
$$u_1(x)=Axe^{-kx}$$
Where A is the normalisation constant.
This works out as:
$$\int_0^{+\infty}u_1^2dx=1$$
$$\int_0^{+\infty}\Big(Axe^{-kx}\Big)^2dx=1$$
$$\int_0^{+\infty}A^2x^2e^{-2kx}dx=1$$
$$A^2\int_0^{+\infty}x^2e^{-2kx}dx=1$$
$$A=2k^{\frac{3}{2}}$$
For the excitations the integrals are a little more complicated and I won't include them here.
Below are the visualised wave functions and electron densities for the first three normalised wave functions:
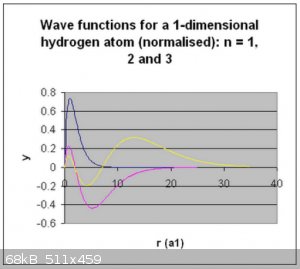
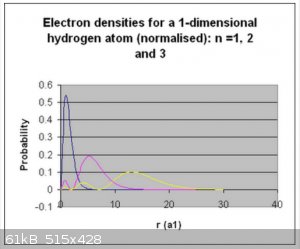
Thanks for reading!
|
|
|
Poppy
Hazard to Others
  
Posts: 294
Registered: 3-11-2011
Member Is Offline
Mood: † chemical zombie
|
|
In my point of view, just as an out of sequence comment, it all begins with stabilishing light waves as analogs of sea waves, that is, energy
fluctuations. Having it in mind, the cosmos can be thought as a very dense energy filled background (vacuum), althought there is no proof favouring or
neglecting it, the fluctuations then interact so strongly at some points that electrons are generated there, and vanquish moments later. The picture
you get is somewhat about electrons having a lifetime around a place which gives then a certain probability of being still present in the observed
time lapse. Thats how you merge the particle and the wave characteristics of the electron and any other particle. Now what makes possible for light
waves alone to interact with themselves is simple gravity.
|
|
|
| Pages:
1
..
31
32
33 |