| Pages:
1
..
10
11
12
13
14
..
19 |
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Doh ! After all that i pressed the wrong calculator buttons at the easy step !
How did you get a number out of the 'transcendental equation' ?
Is there a faster method than Meditiation or Reincarnation ?
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | Doh ! After all that i pressed the wrong calculator buttons at the easy step !
How did you get a number out of the 'transcendental equation' ?
Is there a faster method than Meditiation or Reincarnation ? |
Reincarnation is very slow and takes guts. And then you end up in Cleopatra's body and it all gets very messy!
For 1 variable equations that have no analytical solutions, there exists a myriad of numerical (aka iteration methods), the oldest of which
is probably the Regula Falsi method.
[Edited on 27-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Pretty much maths-saturated at the mo, so i'll file that for Future reading.
Thanks for the reference tho.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
I'll leave the partials till tomorrow then.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Partial Derivatives:
Earlier we saw that the first derivative of a function f(x):
$$f’(x)=\frac{df(x)}{dx}$$
... is the gradient (slope) of that function. So how does that work for a function of two variables, f(x,y), or even three or four? Will there be 2, 3
or 4 gradients?
Let’s look at a simple function f(x,y):
$$z=ax+by+c$$
This is the description of a (flat) plane in three dimensions:
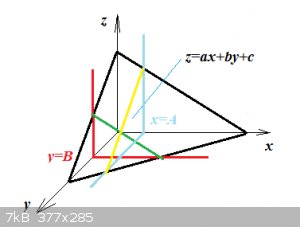
z is the black plane in the pic.
Now we add another plane, this one red:
$$y=B$$
The intersection of the black and red planes is the green line with formula:
$$z=ax+bB+c$$
The first derivative to x of this line is:
$$\frac{dz}{dx}=a+0+0=a$$
This is the gradient of the black plane in the x-direction.
Analogously, if we add another plane, this one light blue:
$$x=A$$
The intersection of the black and light blue planes is the yellow line with formula:
$$z=aA+by+c$$
The first derivative to y of this line is:
$$\frac{dz}{dy}=0+b+0=b$$
This is the gradient of the black plane in the y-direction.
We call these gradients partial derivatives:
$$\frac{\partial z}{\partial x}\:\text{and}\:\frac{\partial z}{\partial y}$$
The partial derivative of z to x is computed by ‘pretending’ y is a constant:
$$\frac{\partial z}{\partial x}=a+0+0=a$$
The partial derivative of z to y is computed by ‘pretending’ x is a constant:
$$\frac{\partial z}{\partial y}=0+b+0=b$$
But this isn’t limited to simple functions like z. It works for ALL functions f(x,y), as a few examples will show:
1.
$$z=3x^2-5y^3$$
$$\frac{\partial z}{\partial x}=6x$$
$$\frac{\partial z}{\partial y}=-15y^2$$
2.
$$u=x^2y+3xy^3-xy$$
$$\frac{\partial u}{\partial x}=2xy+3y^3-y$$
$$\frac{\partial u}{\partial y}=x^2+9xy^2-x$$
3.
$$v=\frac{x}{y} -2\frac{y}{x}$$
$$\frac{\partial v}{\partial x}=\frac1y+2\frac{y}{x^2}$$
$$\frac{\partial v}{\partial y}=-\frac{x}{y^2}-\frac2x$$
4.
$$y=ze^{2x}$$
$$\frac{\partial y}{\partial x}=2ze^{2x}$$
$$\frac{\partial y}{\partial z}=e^{2x}$$
Rules of Partial Derivation:
The rules of partial derivation are exactly the same as for ‘normal’ derivation, including the chain rule. Two examples of the latter:
1.
$$z=\sqrt{x^2-3xy}$$
$$\frac{\partial z}{\partial x}=\frac12 (x^2-3xy)^{-\frac12}\frac{\partial}{\partial x}(x^2-3xy)$$
$$=\frac12 (x^2-3xy)^{-\frac12}(2x-3y)$$
and:
$$\frac{\partial z}{\partial y}=\frac12 (x^2-3xy)^{-\frac12}\frac{\partial}{\partial y}(x^2-3xy)$$
$$=\frac12 (x^2-3xy)^{-\frac12}(-3x)=-\frac32 x(x^2-3xy)^{-\frac12}$$
2.
$$z=e^{x^3-4xy^2}$$
$$\frac{\partial z}{\partial x}=e^{x^3-4xy^2}\frac{\partial}{\partial x}(x^3-4xy^2)$$
$$=e^{x^3-4xy^2}(3x^2-4y^2)$$
and:
$$\frac{\partial z}{\partial y}=e^{x^3-4xy^2}\frac{\partial}{\partial y}(x^3-4xy^2)$$
$$=e^{x^3-4xy^2}(-8xy)=-8xye^{x^3-4xy^2}$$
Partial derivatives of functions dependent on more than two independent variables:
Such a function can generically by represented by:
$$f(x_1,x_2,x_3,...,x_i,...,x_n)$$
For each variable x<sub>i</sub> a partial derivative:
$$\frac{\partial f}{\partial x_i}$$
... can be computed. It's done by considering all other variables (other than x<sub>i</sub> as constants. as constants.
Consider the following example:
$$u(x,y,z)=x^3y+x^2z^2-3zy^2+5xyz$$
$$\frac{\partial u}{\partial x}=3x^2y+2xz^2+5yz$$
$$\frac{\partial u}{\partial y}=x^3-6zy+5xz$$
$$\frac{\partial u}{\partial z}=2x^2z-3y^2+5xy$$
<hr>
I'll let that 'sink in' for a bit and take questions if there are any. Then some simple exercises will be posted.
[Edited on 28-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Cool ! Let's Go !
Haven't gotten anything wrong for Hours now !
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Firstly, a word about notation. The still frequently used:
$$\frac{\partial f}{\partial x}$$
... is fairly clunky (even more so in LaTex), so I propose a more modern and shorter notation:
$$\frac{\partial f}{\partial x}=f_x$$
Example:
$$u=2x-6y^3$$
$$\implies \frac{\partial f}{\partial y}=f_y=-18y^2$$
Exercises: compute f<sub>x</sub> and f<sub>y</sub> for the following (x,y) functions. (I'll put in a trigger
warning, if there's 'danger' ahead).
1.
$$x^2y^3-2xy^4$$
2.
$$\cos x+\sin y$$
3.
$$2xy+\frac{5y}{x}$$
4. (product rule)
$$(x^2-y)(1+y^2)$$
5.
$$x^3y^2-6xy+3x$$
6. (chain rule)
$$\cos(2x-y)$$
7.(product rule + chain rule)
$$x^2\sin (y-x)$$
8. (chain rule)
$$e^{3xy}$$
Enjoy!
[Edited on 28-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Hmm. Best go cautiously then ...
1. $$x^2y^3-2xy^4$$
$$\frac{\partial f}{\partial x}= f_x = 2xy^3-2y^4$$
$$f_y = 3x^2y^2-8xy^3$$
Owzat ?
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Correct. One done, seven more to go.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Hmm. Nothing Bad happened, but it could be a trap.
Let's try the next one
2.
$$\cos x + \sin y$$
$$f_x = sin y - sin x$$
$$f_y = \cos x + cos y$$
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
3.
$$2xy+\frac{5y}{x}$$
$$f_x = 2y - \frac {5y}{x^2}$$
$$f_y = 2x +\frac 5x$$
it feels like i just stepped on a landmine that leapt 10m into the air after i took my foot off, yet failed to explode, just yet.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
4. (geting scared now)
$$(x^2-y)(1+y^2)$$
$$ = (x^2-y)' + (1+y^2)'$$
$$f_x = 2x + y^2$$
$$f_y = x^2 -1 + 2y$$
Gut instinct says it's time to start running.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
5.
$$x^3y^2-6xy+3x$$
$$f_x = 3x^2y^2 - 6y + 3$$
$$f_y = 2x^3y - 6x + 3x$$
Gravy Pressure is pretty much in the Danger Zone now.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
6.
$$\cos(2x-y)$$
$$f_{bleh} = \cos(2x-y)'(2x-y)'$$
$$f_x = -\sin(2x-y)(2-y)$$
$$f_y = -\sin(2x-y)(2x-1)$$
that does not look right, and i think the Gravy Seals are giving way.
[Edited on 28-4-2016 by aga]
[Edited on 28-4-2016 by aga]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
It's no good Heuston. We have Leakage.
Best leave 7 and 8 till the 'morn.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
1. Correct
2. Incorrect.
$$\cos x+\sin y$$
If y is a constant, then so is siny, so:
$$f_x=-\sin x$$
If x is a constant, then so is cosx, so:
$$f_y=\cos y$$
3. Correct
4. (product rule)
Incorrect, you're applying the sum rule, not the product rule. Try:
$$(x^2-y)(1+y^2)$$
$$f_x=f_x(x^2-y) \times (1+y^2)+(x^2-y) \times f_x(1+y^2)$$
Similar for f<sub>y</sub>.
5. fx is correct but fy should be:
$$x^3y^2-6xy+3x$$
$$f_y=2x^3y-6x$$
6. (chain rule)
Almost but not quite:
$$\cos(2x-y)$$
$$f_x=-\sin(2x-y)f_x(2x-y)=2\sin(2x-y)$$
$$f_y=-\sin(2x-y)f_y(2x-y)=-\sin(2x-y)$$
Ok, so we've got some gremlins to deal with. 
[Edited on 28-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Doh. Chain rule is tricky.
7.
$$x^2\sin (y-x)$$
i think it goes like this for the chainy bit:
$$sin(y-x)'(y-x)'$$
$$f_x = (x^2)'sin(y-x)'(y-x)'$$
$$= 2x(-cos(y-x))(-1)$$
$$= 2xcos(y-x)$$
$$f_y = (x^2)(sin(y-x)')(y-x)'$$
$$= x^2(-cos(y-x))(1)$$
$$=-x^2cos(y-x)$$
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
8.
Now these 'e' things really confuse the hell out of me.
$$e^{3xy}$$
the rule says e^n just ends up as e^n, but surely the 3xy needs messing with, so ignoring all the alarm bells, here goes:
$$f_x = e^{3(yx)'(x)'}$$
$$= e^{3y}$$
$$f_y = e^{3x}$$
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
7. (chain rule + product rule)
$$x^2\sin(y-x)$$
You got the chain rule right and thus f<sub>y</sub>. But for f<sub>x</sub> you needed to apply also the product rule because
x<sup>2</sup> is a function, so:
$$f_x=f_x(x^2) \times \sin(y-x)+x^2 \times f_x(\sin(y-x))$$
$$=2x\sin(y-x)+x^2[-\cos(y-x)\times f_x(y-x)]$$
$$=2x\sin(y-x)+\cos(y-x)$$
8. (chain rule)
$$e^{3xy}$$
Here you were a bit all over the place. Remember how to derive exponentials in one variable only, with the chain rule:
$$g=e^{f(x)}$$
$$g'=e^{f(x)}\times f'(x)$$
For an (x,y) exponential:
$$g=e^{f(x,y)}$$
$$g_x=e^{f(x,y)}\times f_x(x,y)$$
$$g_y=e^{f(x,y)}\times f_y(x,y)$$
Applied here:
$$f_x=e^{3xy} \times f_x(3xy)=e^{3xy}(3y)=3ye^{3xy}$$
$$f_y=e^{3xy} \times f_y(3xy)=e^{3xy}(3x)=3xe^{3xy}$$
So definitely some gremlins, not to mention a few missiles going down rather than up!
[Edited on 29-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Beginning to realise that i'm That guy who gets you Rocket Men all the food, lodgings, material, and the booze & hookers every weekend, whilst
earning handsomely from that plus side-rackets.
Then organises the team members' coffins when the Rocket goes sideways and some heads must roll (250% markup on coffins).
Then sells the little i can remember to the Enemy for a Vast fortune (and immunity) once they win the war.
(maybe before, depends on immunity from Whom).
It's pretty much apparent that i was not designed to be a gifted theoretical mathematician.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
It's pretty much apparent that i was not designed to be a gifted theoretical mathematician. |
For most (like me), math is hard work (but rewarding, IMO). So there's few with an excuse ("whoohoo, look at me, I'm sooooo gifted!"), so
what? 
In characteristic human style we'll now just stick our heads in the sand and plow on!
Tomorrow: simple multi-variate optima.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Don't get me wrong :
i actually Like this algebra stuff, just that it's pretty clear that i'm not careful or thoughtful enough for such a Precise discipline.
Chemistry should be fine as i have Buckets to mix stuff up in 
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Multi-variate optima:
Higher up we saw that for a simple function f(x), an optimum exists, if:
$$\frac{df(x)}{dx}=0$$
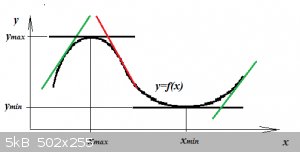
Similarly, a multivariate function:
$$f(x_1,x_2,...,x_i,...,x_n)$$
... has an optimum if:
$$f_{x_1}=0,f_{x_n}=0,...,f_{x_n}=0,$$
The latter condition forms a system of simultaneous equations which when solved yields the numerical values x<sub>i</sub> of the optimum.
We won't concern ourselves here with the formal theory of multi-variate optima (which includes detection of absolute and relative extremes and saddle
points), instead we'll use common sense to determine whether a found optimum is a maximum or minimum.
First example:
$$f(x,y)=x^2+y^2$$
$$f_x=2x$$
$$f_y=2y$$
An optimum exists for:
$$2x=0 \implies x=0$$
$$2y=0 \implies y=0$$
The optimum value is:
$$f(0,0)=0$$
For slightly larger values of x and y, e.g. (1,1), we get:
$$f(1,1)=2$$
... which indicates (0,0) is a minimum.
Second example:
$$x^2+2y^2-xy+14y$$
$$f_x=2x-y=0 \implies y=2x$$
$$f_y=4y-x+14=0 \implies 8x-x=-14$$
$$x=-2, y=-4$$
3D plot:
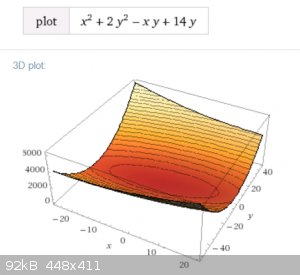
Third example:
$$f(x,y)=xy+\frac8x+\frac8y$$
$$f_x=y-\frac{8}{x^2}=0$$
$$f_y=x-\frac{8}{y^2}=0$$
Some reworking and substituting:
$$y=\frac{8}{x^2}$$
$$x-\frac{x^4}{8}=0$$
$$x(1-\frac{x^3}{8})=0$$
$$1-\frac{x^3}{8}=0$$
$$x=2$$
$$y=2$$
$$f(2,2)=4+4+4=12$$
$$f(4,4)=16+2+2=18$$
(2,2) is a minimum.
Exercise:
$$f(x,y)=(x-1)^2+y^3-3y^2-9y+5$$
[Edited on 30-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Um. Er. Ok. Find the f(x,y) = 0 ?
$$f(x,y)=(x-1)^2+y^3-3y^2-9y+5$$
$$=x^2-2x+1+y^3-3y^2-9y+5$$
$$f_x = 2x-2+0-0-0+0$$
$$ = 2x - 2$$
$$2x-2 = 0 $$
$$\therefore x=1$$
$$f_y = 0-0+0+3y^2-6y-9+0$$
$$=y^2-2y-3$$
$$=y(y-2)-3$$
$$y(y-2)-3 = 0$$
$$y(y-2)=3$$
$$\therefore y = 3$$
$$\implies f(x,y) = 0 = f(1,3)$$
that very last bit was more common sense and trying some numbers than actual maths.
Did i just become Cleopatra ? If so, bathe your ass in milk immediately.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
aga:
Both partial derivatives were correct.
So is x = 1.
But your attempt at solving:
$$y^2-2y-3=0$$
... was very '#creative#' but not very correct!  
No, it does not imply that if:
$$y(y-2)=3$$
... then:
$$y=3$$
For a general quadratic equation:
$$ax^2+bx+c=0$$
$$\implies x_{1,2}=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$$
So we have two roots:
$$y=3,y=-1$$
So we have two optima, (1,-1), a maximum and (1,3), a minimum, as the 3D plot shows:

[Edited on 30-4-2016 by blogfast25]
|
|
|
| Pages:
1
..
10
11
12
13
14
..
19 |